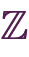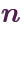第2話では、集合と自然数と加算の公理を使って「



 」を証明しました。 しかし、これらの公理を持ち出さなくてもわたしたちは「
」を証明しました。 しかし、これらの公理を持ち出さなくてもわたしたちは「



 」であることを確信しています。 そこで、前回のような方法で「
」であることを確信しています。 そこで、前回のような方法で「



 」や「
」や「



 」などを証明していくことはやめ、その気になればこれらも証明可能であるとした上で、今後は「本当に成り立つかどうか判らないこと」に焦点を当てて進めることにします。
」などを証明していくことはやめ、その気になればこれらも証明可能であるとした上で、今後は「本当に成り立つかどうか判らないこと」に焦点を当てて進めることにします。




 」を証明しました。 しかし、これらの公理を持ち出さなくてもわたしたちは「
」を証明しました。 しかし、これらの公理を持ち出さなくてもわたしたちは「



 」であることを確信しています。 そこで、前回のような方法で「
」であることを確信しています。 そこで、前回のような方法で「



 」や「
」や「



 」などを証明していくことはやめ、その気になればこれらも証明可能であるとした上で、今後は「本当に成り立つかどうか判らないこと」に焦点を当てて進めることにします。
」などを証明していくことはやめ、その気になればこれらも証明可能であるとした上で、今後は「本当に成り立つかどうか判らないこと」に焦点を当てて進めることにします。1.整数
 より大きい数を「正(せい)」の数といい、
より大きい数を「正(せい)」の数といい、 より小さい数を「負(ふ)」の数といいます。
より小さい数を「負(ふ)」の数といいます。  はどちらでもありません。
はどちらでもありません。どのような2つの整数

 に対しても、加算「
に対しても、加算「

 」や減算「
」や減算「

 」や乗算「
」や乗算「

 」が行えることはご存知の通りです。 「
」が行えることはご存知の通りです。 「

 」は「
」は「

 」と書かれたり、しばしば乗算の記号が省略されて「
」と書かれたり、しばしば乗算の記号が省略されて「
 」と書かれます。 この記事でも、これ以降はそのように書いていきます。
」と書かれます。 この記事でも、これ以降はそのように書いていきます。


 に対しても、加算「
に対しても、加算「

 」や減算「
」や減算「

 」や乗算「
」や乗算「

 」が行えることはご存知の通りです。 「
」が行えることはご存知の通りです。 「

 」は「
」は「

 」と書かれたり、しばしば乗算の記号が省略されて「
」と書かれたり、しばしば乗算の記号が省略されて「
 」と書かれます。 この記事でも、これ以降はそのように書いていきます。
」と書かれます。 この記事でも、これ以降はそのように書いていきます。1.1累乗
整数 と、
と、 以上の整数
以上の整数 に対し、「
に対し、「 を
を 回掛けた数」を「
回掛けた数」を「
 」と表して「累乗(るいじょう)」といいます。 例えば「
」と表して「累乗(るいじょう)」といいます。 例えば「
 」は「
」は「



 」、つまり
」、つまり です。 「
です。 「

 」は「
」は「









 」、つまり
」、つまり



 です。
です。
 と、
と、 以上の整数
以上の整数 に対し、「
に対し、「 を
を 回掛けた数」を「
回掛けた数」を「
 」と表して「累乗(るいじょう)」といいます。 例えば「
」と表して「累乗(るいじょう)」といいます。 例えば「
 」は「
」は「



 」、つまり
」、つまり です。 「
です。 「

 」は「
」は「









 」、つまり
」、つまり



 です。
です。ただし、 でない任意の数
でない任意の数 に対し、「
に対し、「


 」とします。 例えば「
」とします。 例えば「


 」「
」「





 」です。
」です。
 でない任意の数
でない任意の数 に対し、「
に対し、「


 」とします。 例えば「
」とします。 例えば「


 」「
」「





 」です。
」です。補足
「2⁵ = 32」「2⁴ = 16」「2³ = 8」「2² = 4」「2¹ = 2」と見ていくと、結果が半分ずつになっていっているため、「2⁰ = 1」と考えることが自然だと分かります。
「
 」は、便宜上「
」は、便宜上「 」と定義されることもありますが、様々な理由から多くの場合には定義されません。
」と定義されることもありますが、様々な理由から多くの場合には定義されません。

 」は、便宜上「
」は、便宜上「 」と定義されることもありますが、様々な理由から多くの場合には定義されません。
」と定義されることもありますが、様々な理由から多くの場合には定義されません。補足
「0⁰」が通常定義されない理由の1つは、「3⁰ = 1」「2⁰ = 1」「1⁰ = 1」と見ていくと「0⁰ = 1」と考えることが自然なのに対し、「0³ = 0」「0² = 0」「0¹ = 0」と見ていくと「0⁰ = 0」と考えることが自然となって食い違うためです。
累乗には下記の法則が成り立ちます。
(1)は、「





 (
( が
が 個)」と「
個)」と「





 (
( が
が 個)」を掛けると、全部で「
個)」を掛けると、全部で「





 (
( が
が

 個)」になることから明らかです。
個)」になることから明らかです。






 (
( が
が 個)」と「
個)」と「





 (
( が
が 個)」を掛けると、全部で「
個)」を掛けると、全部で「





 (
( が
が

 個)」になることから明らかです。
個)」になることから明らかです。(2)は、割り算によって の個数が減るため、
の個数が減るため、 の数が引き算になります。
の数が引き算になります。
 の個数が減るため、
の個数が減るため、 の数が引き算になります。
の数が引き算になります。(3)は、「





 (
( が
が 個)」自体が
個)」自体が 個あるということなので、「
個あるということなので、「





 (
( が
が

 個)」となります。
個)」となります。






 (
( が
が 個)」自体が
個)」自体が 個あるということなので、「
個あるということなので、「





 (
( が
が

 個)」となります。
個)」となります。(4)は、「











 (
( と
と がそれぞれ
がそれぞれ 個ずつ)」なので、順番を入れ替えて「
個ずつ)」なので、順番を入れ替えて「













 (
( と
と がそれぞれ
がそれぞれ 個ずつ)」となります。
個ずつ)」となります。












 (
( と
と がそれぞれ
がそれぞれ 個ずつ)」なので、順番を入れ替えて「
個ずつ)」なので、順番を入れ替えて「













 (
( と
と がそれぞれ
がそれぞれ 個ずつ)」となります。
個ずつ)」となります。1.2絶対値
さて、整数 が
が からどれだけ離れているかを、
からどれだけ離れているかを、 の「絶対値(ぜったいち)」といい、「
の「絶対値(ぜったいち)」といい、「

 」と表します。 例えば
」と表します。 例えば の絶対値は「
の絶対値は「



 」、
」、
 の絶対値は「
の絶対値は「




 」です。
」です。
 が
が からどれだけ離れているかを、
からどれだけ離れているかを、 の「絶対値(ぜったいち)」といい、「
の「絶対値(ぜったいち)」といい、「

 」と表します。 例えば
」と表します。 例えば の絶対値は「
の絶対値は「



 」、
」、
 の絶対値は「
の絶対値は「




 」です。
」です。絶対値とは、「正の数のときはそのままで、負の数のときはマイナスを取った数」と考えても良いでしょう。
より厳密に定義すると、下記の通りです。
以下を満たす

 を
を の絶対値という。
の絶対値という。


 のとき、
のとき、



 。
。

 のとき、
のとき、




 。
。
例えば


 の場合、
の場合、

 なので、
なので、












 です。
です。



 の場合、
の場合、

 なので、
なので、












 です。
です。2.整数の性質
さて、ここからは整数の様々な性質について解説します。
2.1商と余り
2つの整数の除算(

 )は、その値が整数にならないことがあります。 そこで、計算結果が整数になる「商(しょう)」と「余(あま)り」というものを定義します。
)は、その値が整数にならないことがあります。 そこで、計算結果が整数になる「商(しょう)」と「余(あま)り」というものを定義します。


 )は、その値が整数にならないことがあります。 そこで、計算結果が整数になる「商(しょう)」と「余(あま)り」というものを定義します。
)は、その値が整数にならないことがあります。 そこで、計算結果が整数になる「商(しょう)」と「余(あま)り」というものを定義します。「

 」をしたとき、「商」とは、
」をしたとき、「商」とは、 個のものを
個のものを 人に配ったときの1人あたりの個数のことです。 「余り」は、配りきれずに残った個数です。 例えば、「
人に配ったときの1人あたりの個数のことです。 「余り」は、配りきれずに残った個数です。 例えば、「

 」の商は
」の商は 、余りは
、余りは です。
です。


 」をしたとき、「商」とは、
」をしたとき、「商」とは、 個のものを
個のものを 人に配ったときの1人あたりの個数のことです。 「余り」は、配りきれずに残った個数です。 例えば、「
人に配ったときの1人あたりの個数のことです。 「余り」は、配りきれずに残った個数です。 例えば、「

 」の商は
」の商は 、余りは
、余りは です。
です。「

 の商は
の商は 、余りは
、余りは 」とは「
」とは「 個のものを
個のものを 人に配ったとき、1人あたり
人に配ったとき、1人あたり 個ずつになり
個ずつになり 個余る」ということと言えますが、言い換えると「1人あたり
個余る」ということと言えますが、言い換えると「1人あたり 個のものが、
個のものが、 人分あり、それと余りの
人分あり、それと余りの 個を合わせると
個を合わせると 個になる」ことと同じです。 これは「
個になる」ことと同じです。 これは「





 」と書けます。 つまり、「
」と書けます。 つまり、「

 の商
の商 と余り
と余り 」とは、「
」とは、「





 」を満たす数と定義できます。
」を満たす数と定義できます。


 の商は
の商は 、余りは
、余りは 」とは「
」とは「 個のものを
個のものを 人に配ったとき、1人あたり
人に配ったとき、1人あたり 個ずつになり
個ずつになり 個余る」ということと言えますが、言い換えると「1人あたり
個余る」ということと言えますが、言い換えると「1人あたり 個のものが、
個のものが、 人分あり、それと余りの
人分あり、それと余りの 個を合わせると
個を合わせると 個になる」ことと同じです。 これは「
個になる」ことと同じです。 これは「





 」と書けます。 つまり、「
」と書けます。 つまり、「

 の商
の商 と余り
と余り 」とは、「
」とは、「





 」を満たす数と定義できます。
」を満たす数と定義できます。整数 と、
と、 以外の整数
以外の整数 に対し、「
に対し、「

 」をしたときの商と余りとは、それぞれ「
」をしたときの商と余りとは、それぞれ「





 および
および



 」を満たす整数
」を満たす整数 と
と と定義する。
と定義する。
例えば「

 」を考えると、商が
」を考えると、商が 、余り
、余り になりますが、上記の式の
になりますが、上記の式の に
に 、
、 に
に 、商
、商 に
に 、余り
、余り に
に を入れると「
を入れると「





 および
および



 」となり、確かに数式を満たしていることが分かります。
」となり、確かに数式を満たしていることが分かります。


 」を考えると、商が
」を考えると、商が 、余り
、余り になりますが、上記の式の
になりますが、上記の式の に
に 、
、 に
に 、商
、商 に
に 、余り
、余り に
に を入れると「
を入れると「





 および
および



 」となり、確かに数式を満たしていることが分かります。
」となり、確かに数式を満たしていることが分かります。上記の式で が
が のときの商や余りは定義されません。 つまり「
のときの商や余りは定義されません。 つまり「

 」などは定義されません。
」などは定義されません。
 が
が のときの商や余りは定義されません。 つまり「
のときの商や余りは定義されません。 つまり「

 」などは定義されません。
」などは定義されません。2.2割り切る、約数、倍数
「

 」の余りが
」の余りが であれば、「
であれば、「 は
は を割(わ)り切(き)る」といいます。 例えば「
を割(わ)り切(き)る」といいます。 例えば「

 」は余りが
」は余りが なので、
なので、 は
は を割り切ります。 また「
を割り切ります。 また「


 」も余りが
」も余りが なので、
なので、 は
は
 を割り切ります。
を割り切ります。


 」の余りが
」の余りが であれば、「
であれば、「 は
は を割(わ)り切(き)る」といいます。 例えば「
を割(わ)り切(き)る」といいます。 例えば「

 」は余りが
」は余りが なので、
なので、 は
は を割り切ります。 また「
を割り切ります。 また「


 」も余りが
」も余りが なので、
なので、 は
は
 を割り切ります。
を割り切ります。そして は
は を割り切るとき、
を割り切るとき、 は
は の「約数(やくすう)」といい、また
の「約数(やくすう)」といい、また は
は の「倍数(ばいすう)」といいます。 例えば
の「倍数(ばいすう)」といいます。 例えば は
は を割り切るため、
を割り切るため、 は
は の約数で、
の約数で、 は
は の倍数です。
の倍数です。
 は
は を割り切るとき、
を割り切るとき、 は
は の「約数(やくすう)」といい、また
の「約数(やくすう)」といい、また は
は の「倍数(ばいすう)」といいます。 例えば
の「倍数(ばいすう)」といいます。 例えば は
は を割り切るため、
を割り切るため、 は
は の約数で、
の約数で、 は
は の倍数です。
の倍数です。また、
 の約数とは、
の約数とは、
 を割り切る数なので小さい順に列挙すると、「
を割り切る数なので小さい順に列挙すると、「





























 」となります。 また、
」となります。 また、 の倍数とは、「
の倍数とは、「

















 」となり、つまり偶数全体になります。
」となり、つまり偶数全体になります。

 の約数とは、
の約数とは、
 を割り切る数なので小さい順に列挙すると、「
を割り切る数なので小さい順に列挙すると、「





























 」となります。 また、
」となります。 また、 の倍数とは、「
の倍数とは、「

















 」となり、つまり偶数全体になります。
」となり、つまり偶数全体になります。 と
と
 はすべての整数を割り切るため、
はすべての整数を割り切るため、 の倍数や
の倍数や
 の倍数は整数全体になります。
の倍数は整数全体になります。  を除くすべての整数は
を除くすべての整数は を割り切るため、
を割り切るため、 の約数は、
の約数は、 を除く整数全体になります。
を除く整数全体になります。2.3公約数、公倍数
さて、2つ以上の整数の、共通の約数と倍数を考えましょう。
 と
と の共通の約数のことを、
の共通の約数のことを、 と
と の「公約数(こうやくすう)」といいます。 言い換えると、
の「公約数(こうやくすう)」といいます。 言い換えると、 は
は を割り切り、
を割り切り、 は
は を割り切るとき、整数
を割り切るとき、整数 を、
を、 と
と の「公約数」といいます。 例えば、
の「公約数」といいます。 例えば、 は
は を割り切り、
を割り切り、 は
は を割り切るので、
を割り切るので、 は
は と
と の公約数の1つです。
の公約数の1つです。 と
と の共通の倍数のことを、
の共通の倍数のことを、 と
と の「公倍数(こうばいすう)」といいます。 言い換えると、
の「公倍数(こうばいすう)」といいます。 言い換えると、 は
は を割り切り、
を割り切り、 は
は を割り切るとき、整数
を割り切るとき、整数 を、
を、 と
と の「公倍数」といいます。 例えば、
の「公倍数」といいます。 例えば、 は
は
 を割り切り、
を割り切り、 は
は
 を割り切るので、
を割り切るので、
 は
は と
と の公倍数の1つです。
の公倍数の1つです。3つ以上の数についても、共通の約数や倍数を考えることで、それらの公約数、公倍数が定義できます。
2.4最大公約数と最小公倍数
 と
と の公約数のうち最大のものを、
の公約数のうち最大のものを、 と
と の「最大公約数(さいだいこうやくすう)」といい、よく「
の「最大公約数(さいだいこうやくすう)」といい、よく「






 」と表します。 また、
」と表します。 また、 と
と の正の公倍数のうち最小のものを、
の正の公倍数のうち最小のものを、 と
と の「最小公倍数(さいしょうこうばいすう)」といい、よく「
の「最小公倍数(さいしょうこうばいすう)」といい、よく「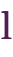






 」と表します。
」と表します。補足
gcdは「greatest common divisor (最大公約数)」の略、lcmは「least common multiple (最小公倍数)」の略です。
例えば、 の約数は全部で「
の約数は全部で「

















 」で、
」で、 の約数は全部で「
の約数は全部で「

















 」です。 このとき、
」です。 このとき、 と
と の公約数は共通の「
の公約数は共通の「







 」となり、最大公約数はそのうち最大のものなので、
」となり、最大公約数はそのうち最大のものなので、








 です。
です。
 の約数は全部で「
の約数は全部で「

















 」で、
」で、 の約数は全部で「
の約数は全部で「

















 」です。 このとき、
」です。 このとき、 と
と の公約数は共通の「
の公約数は共通の「







 」となり、最大公約数はそのうち最大のものなので、
」となり、最大公約数はそのうち最大のものなので、








 です。
です。また、 の正の倍数は「
の正の倍数は「










 」で、
」で、 の正の倍数は「
の正の倍数は「













 」です。 このとき、
」です。 このとき、 と
と の正の公倍数は共通の「
の正の公倍数は共通の「








 」となり、最小公倍数はそのうち最小のものなので、
」となり、最小公倍数はそのうち最小のものなので、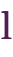









 です。
です。
 の正の倍数は「
の正の倍数は「










 」で、
」で、 の正の倍数は「
の正の倍数は「













 」です。 このとき、
」です。 このとき、 と
と の正の公倍数は共通の「
の正の公倍数は共通の「








 」となり、最小公倍数はそのうち最小のものなので、
」となり、最小公倍数はそのうち最小のものなので、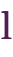









 です。
です。正の整数

 に対して、「
に対して、「












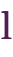






 」が成り立つという法則があります。 例えば、「
」が成り立つという法則があります。 例えば、「










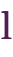









 」でしたので、「
」でしたので、「












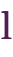






 」に代入して「
」に代入して「






 」より「
」より「



 」となって成り立っていることが分かります。 これを使えば、最大公約数と最小公倍数のどちらかが分かればもう一方は簡単に計算できます。
」となって成り立っていることが分かります。 これを使えば、最大公約数と最小公倍数のどちらかが分かればもう一方は簡単に計算できます。


 に対して、「
に対して、「












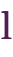






 」が成り立つという法則があります。 例えば、「
」が成り立つという法則があります。 例えば、「










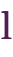









 」でしたので、「
」でしたので、「












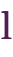






 」に代入して「
」に代入して「






 」より「
」より「



 」となって成り立っていることが分かります。 これを使えば、最大公約数と最小公倍数のどちらかが分かればもう一方は簡単に計算できます。
」となって成り立っていることが分かります。 これを使えば、最大公約数と最小公倍数のどちらかが分かればもう一方は簡単に計算できます。2.5ユークリッドの互除法
最大公約数を安直に求めると時間がかかりますが、以下に示した「ユークリッドの互除法(ごじょほう)」という方法を使うと早く求まります。
- 最大公約数を求めたい2つの整数のうち、大きいほうを
 、小さいほうを
、小さいほうを とおく。
とおく。 

 の余りを
の余りを とおく。
とおく。- このとき


 であれば、
であれば、 と
と の最大公約数は、
の最大公約数は、 と
と の最大公約数に等しい。 よって、
の最大公約数に等しい。 よって、 と
と の最大公約数を求めることにして(1)に戻る。
の最大公約数を求めることにして(1)に戻る。 - 一方で


 であれば、
であれば、 と
と の最大公約数は、
の最大公約数は、 である。(計算終了)
である。(計算終了)
例えば、

 と
と
 の最大公約数をユークリッドの互除法で求めた結果は、下記の通りです。
の最大公約数をユークリッドの互除法で求めた結果は、下記の通りです。


 と
と
 の最大公約数をユークリッドの互除法で求めた結果は、下記の通りです。
の最大公約数をユークリッドの互除法で求めた結果は、下記の通りです。

 と
と
 のうち、大きいほうは
のうち、大きいほうは

 、小さいほうは
、小さいほうは
 なので、
なので、



 、
、


 とおく。
とおく。

 つまり
つまり




 の余りは、
の余りは、


 なので、「
なので、「 と
と の最大公約数は、
の最大公約数は、 と
と の最大公約数に等しい」ことにより、
の最大公約数に等しい」ことにより、




















 。
。- 同様に、



 、
、


 として繰り返すと、
として繰り返すと、






























 。
。 - ここで、




 の余りは
の余りは

 なので、
なので、








 より、
より、











 。
。 - よって、













 。
。
一般的には、共通の約数を列挙するよりも単に割り算を繰り返すほうが簡単なので、この方法が便利になります。
3.素数
正の約数が と
と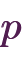 だけである、
だけである、 以上の整数
以上の整数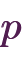 のことを、「素数(そすう)」といいます。 例えば
のことを、「素数(そすう)」といいます。 例えば は、正の約数が
は、正の約数が と
と だけなので素数です。
だけなので素数です。  は、正の約数が
は、正の約数が と
と の他に
の他に もあるため、素数ではありません。
もあるため、素数ではありません。
 と
と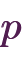 だけである、
だけである、 以上の整数
以上の整数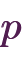 のことを、「素数(そすう)」といいます。 例えば
のことを、「素数(そすう)」といいます。 例えば は、正の約数が
は、正の約数が と
と だけなので素数です。
だけなので素数です。  は、正の約数が
は、正の約数が と
と の他に
の他に もあるため、素数ではありません。
もあるため、素数ではありません。言い換えると素数とは、 以上の整数のうち、「『
以上の整数のうち、「『 と自分自身』以外の正の整数では割り切れない数」のことです。 素数でない
と自分自身』以外の正の整数では割り切れない数」のことです。 素数でない 以上の整数を「合成数(ごうせいすう)」といいます。
以上の整数を「合成数(ごうせいすう)」といいます。
 以上の整数のうち、「『
以上の整数のうち、「『 と自分自身』以外の正の整数では割り切れない数」のことです。 素数でない
と自分自身』以外の正の整数では割り切れない数」のことです。 素数でない 以上の整数を「合成数(ごうせいすう)」といいます。
以上の整数を「合成数(ごうせいすう)」といいます。素数を小さい順に並べると「

























 」と続いていきます。 素数は無限に存在します。 また、素数の現れ方は不規則に見え、その規則を捉えるための研究が古代から現在にいたるまで続いています。
」と続いていきます。 素数は無限に存在します。 また、素数の現れ方は不規則に見え、その規則を捉えるための研究が古代から現在にいたるまで続いています。


























 」と続いていきます。 素数は無限に存在します。 また、素数の現れ方は不規則に見え、その規則を捉えるための研究が古代から現在にいたるまで続いています。
」と続いていきます。 素数は無限に存在します。 また、素数の現れ方は不規則に見え、その規則を捉えるための研究が古代から現在にいたるまで続いています。素数は、「エラトステネスの篩(ふるい)」という方法で得ることができます。 これは「 以上の整数のうち、他の素数の倍数でないものは素数である」ことを利用した方法で、下記のように行います。
以上の整数のうち、他の素数の倍数でないものは素数である」ことを利用した方法で、下記のように行います。
 以上の整数のうち、他の素数の倍数でないものは素数である」ことを利用した方法で、下記のように行います。
以上の整数のうち、他の素数の倍数でないものは素数である」ことを利用した方法で、下記のように行います。
3.1素因数分解
すべての正の整数は、素数の積(掛け算)で表すことができます。 例えば、「



 」「
」「



 」「
」「






 」などです。 このように正の整数を素数の積で表すことを、「素因数分解(そいんすうぶんかい)」といいます。
」などです。 このように正の整数を素数の積で表すことを、「素因数分解(そいんすうぶんかい)」といいます。




 」「
」「



 」「
」「






 」などです。 このように正の整数を素数の積で表すことを、「素因数分解(そいんすうぶんかい)」といいます。
」などです。 このように正の整数を素数の積で表すことを、「素因数分解(そいんすうぶんかい)」といいます。また素因数分解したときに現れるそれぞれの素数を「素因数(そいんすう)」といいます。 例えば「




 」なので、
」なので、
 の素因数は
の素因数は と
と です。
です。





 」なので、
」なので、
 の素因数は
の素因数は と
と です。
です。どの正の整数も必ず素因数分解することができ、そのパターンは、積の順序を無視すれば1通りに限られます。 例えば累乗を使って表すと、「







 」「
」「







 」「
」「







 」「
」「







 」「
」「







 」「
」「







 」のようになります。 この性質は「素因数分解(そいんすうぶんかい)の一意性(いちいせい)」と呼ばれ、他の定理を証明するのに役立ちます。
」のようになります。 この性質は「素因数分解(そいんすうぶんかい)の一意性(いちいせい)」と呼ばれ、他の定理を証明するのに役立ちます。








 」「
」「







 」「
」「







 」「
」「







 」「
」「







 」「
」「







 」のようになります。 この性質は「素因数分解(そいんすうぶんかい)の一意性(いちいせい)」と呼ばれ、他の定理を証明するのに役立ちます。
」のようになります。 この性質は「素因数分解(そいんすうぶんかい)の一意性(いちいせい)」と呼ばれ、他の定理を証明するのに役立ちます。素数に「 」を含めない理由は、
」を含めない理由は、 を素数に含めると、「
を素数に含めると、「























 」となって、素因数分解の一意性が成り立たなくなるためです。
」となって、素因数分解の一意性が成り立たなくなるためです。
 」を含めない理由は、
」を含めない理由は、 を素数に含めると、「
を素数に含めると、「























 」となって、素因数分解の一意性が成り立たなくなるためです。
」となって、素因数分解の一意性が成り立たなくなるためです。3.2互いに素
2つの整数 と
と が、
が、 と
と
 以外に公約数を持たないとき、すなわち
以外に公約数を持たないとき、すなわち








 のとき、
のとき、 と
と は「互(たが)いに素(そ)」であるといいます。 例えば
は「互(たが)いに素(そ)」であるといいます。 例えば









 なので、
なので、 と
と
 は互いに素です。
は互いに素です。
 と
と が、
が、 と
と
 以外に公約数を持たないとき、すなわち
以外に公約数を持たないとき、すなわち








 のとき、
のとき、 と
と は「互(たが)いに素(そ)」であるといいます。 例えば
は「互(たが)いに素(そ)」であるといいます。 例えば









 なので、
なので、 と
と
 は互いに素です。
は互いに素です。正の整数 と
と が「互いに素」であるとは、
が「互いに素」であるとは、 と
と に「共通の素因数がない」ことと同値です。 例えば、
に「共通の素因数がない」ことと同値です。 例えば、



 、
、






 より、
より、 と
と
 には共通の素因数が含まれていないため互いに素といえます。
には共通の素因数が含まれていないため互いに素といえます。
 と
と が「互いに素」であるとは、
が「互いに素」であるとは、 と
と に「共通の素因数がない」ことと同値です。 例えば、
に「共通の素因数がない」ことと同値です。 例えば、



 、
、






 より、
より、 と
と
 には共通の素因数が含まれていないため互いに素といえます。
には共通の素因数が含まれていないため互いに素といえます。4.合同式
さて、割り算の余りの話に戻りますが、「 を
を で割った余りは
で割った余りは 」で、「
」で、「 を
を で割った余りも
で割った余りも 」で、一致しています。 これは、「整数を
」で、一致しています。 これは、「整数を で割った余りの世界では
で割った余りの世界では

 が成り立っている」と言えるでしょう。 このように
が成り立っている」と言えるでしょう。 このように で割った余りが一致しているとき、「
で割った余りが一致しているとき、「 と
と は
は を法(ほう)として合同(ごうどう)」といい、「
を法(ほう)として合同(ごうどう)」といい、「







 」と書きます。
」と書きます。
 を
を で割った余りは
で割った余りは 」で、「
」で、「 を
を で割った余りも
で割った余りも 」で、一致しています。 これは、「整数を
」で、一致しています。 これは、「整数を で割った余りの世界では
で割った余りの世界では

 が成り立っている」と言えるでしょう。 このように
が成り立っている」と言えるでしょう。 このように で割った余りが一致しているとき、「
で割った余りが一致しているとき、「 と
と は
は を法(ほう)として合同(ごうどう)」といい、「
を法(ほう)として合同(ごうどう)」といい、「







 」と書きます。
」と書きます。また一般に、

 と
と

 の余りが一致しているとき、「
の余りが一致しているとき、「 と
と は
は を法として合同」といい、「
を法として合同」といい、「







 」と書きます。 一致していないときは「
」と書きます。 一致していないときは「







 」と書きます。 このように書いた式を「合同式(ごうどうしき)」といいます。
」と書きます。 このように書いた式を「合同式(ごうどうしき)」といいます。


 と
と

 の余りが一致しているとき、「
の余りが一致しているとき、「 と
と は
は を法として合同」といい、「
を法として合同」といい、「







 」と書きます。 一致していないときは「
」と書きます。 一致していないときは「







 」と書きます。 このように書いた式を「合同式(ごうどうしき)」といいます。
」と書きます。 このように書いた式を「合同式(ごうどうしき)」といいます。例えば、「 を
を で割った余り」は「
で割った余り」は「 を
を で割った余り」と同じなので、「
で割った余り」と同じなので、「







 」となります。 一方「
」となります。 一方「 を
を で割った余り」は「
で割った余り」は「 を
を で割った余り」と異なるので、「
で割った余り」と異なるので、「







 」となります。
」となります。
 を
を で割った余り」は「
で割った余り」は「 を
を で割った余り」と同じなので、「
で割った余り」と同じなので、「







 」となります。 一方「
」となります。 一方「 を
を で割った余り」は「
で割った余り」は「 を
を で割った余り」と異なるので、「
で割った余り」と異なるので、「







 」となります。
」となります。合同式は、両辺に同じ数を足したり引いたり掛けたりしても成立する性質があります。
任意の整数



 に対し、
に対し、







 が成り立つとき、以下の(1)から(3)が成り立つ。
が成り立つとき、以下の(1)から(3)が成り立つ。
- 任意の整数
 に対し、
に対し、











 。
。 - 任意の整数
 に対し、
に対し、











 。
。 - 任意の整数
 に対し、
に対し、











 。
。
例えば、「







 」が成り立ちましたので、両辺を
」が成り立ちましたので、両辺を

 倍して「
倍して「











 」も成り立ちます。
」も成り立ちます。








 」が成り立ちましたので、両辺を
」が成り立ちましたので、両辺を

 倍して「
倍して「











 」も成り立ちます。
」も成り立ちます。5.不定方程式
それでは最後に、今までに紹介した整数の性質を応用した具体的な問題に挑戦してみましょう。 「不定方程式(ふていほうていしき)」と呼ばれる問題です。
「方程式(ほうていしき)」とは、「


 を満たす
を満たす を求めよ」のような、等式を成立させる変数の値を求める問題のことです。 このとき、等式が成立するような変数の値のことを、方程式の「解(かい)」といいます。
を求めよ」のような、等式を成立させる変数の値を求める問題のことです。 このとき、等式が成立するような変数の値のことを、方程式の「解(かい)」といいます。



 を満たす
を満たす を求めよ」のような、等式を成立させる変数の値を求める問題のことです。 このとき、等式が成立するような変数の値のことを、方程式の「解(かい)」といいます。
を求めよ」のような、等式を成立させる変数の値を求める問題のことです。 このとき、等式が成立するような変数の値のことを、方程式の「解(かい)」といいます。方程式のうち「不定方程式」とは、方程式の解が無数にあるものを指します。 例えば「


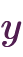

 を満たす
を満たす と
と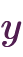 の組み合わせを求めよ」のようなものです。 この場合、「
の組み合わせを求めよ」のようなものです。 この場合、「



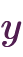

 」や「
」や「



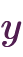

 」などが解となります。
」などが解となります。



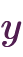

 を満たす
を満たす と
と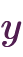 の組み合わせを求めよ」のようなものです。 この場合、「
の組み合わせを求めよ」のようなものです。 この場合、「



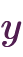

 」や「
」や「



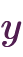

 」などが解となります。
」などが解となります。このように不定方程式では方程式の解が無数にありますが、条件を付けることで、解の個数が有限個になることがあります。 今回はその条件を利用することで、パズルのように解ける問題を見ていきましょう。
5.1問題
それでは不定方程式の具体的な問題として、以下に挑戦しましょう。
問題



 を
を


 とすることを「逆順にする」ということにする。 このとき、ある
とすることを「逆順にする」ということにする。 このとき、ある 桁の整数
桁の整数 を逆順にすると、もとの数
を逆順にすると、もとの数 の
の 倍になった。
倍になった。  の値を求めよ。
の値を求めよ。
5.2解法
まずは、不定方程式を組み立てましょう。  桁の整数
桁の整数 を上の桁から1桁ずつ
を上の桁から1桁ずつ 、
、 、
、 、
、 と置きます。 例えば、
と置きます。 例えば、




 の場合は
の場合は

 、
、

 、
、

 、
、

 です。 すると、
です。 すると、 は
は














 と表せます。
と表せます。
 桁の整数
桁の整数 を上の桁から1桁ずつ
を上の桁から1桁ずつ 、
、 、
、 、
、 と置きます。 例えば、
と置きます。 例えば、




 の場合は
の場合は

 、
、

 、
、

 、
、

 です。 すると、
です。 すると、 は
は














 と表せます。
と表せます。このとき、逆順にしたときに元の数の 倍になることから、以下の方程式が出来上がります。
倍になることから、以下の方程式が出来上がります。
 倍になることから、以下の方程式が出来上がります。
倍になることから、以下の方程式が出来上がります。




































左辺は を
を 倍した数、右辺は
倍した数、右辺は を逆順にした数です。
を逆順にした数です。
 を
を 倍した数、右辺は
倍した数、右辺は を逆順にした数です。
を逆順にした数です。このままではこの式は4つの変数を含んだ不定方程式で解が無数に存在しますので、様々な条件を利用して解を絞り込んでいきましょう。
5.3aの値を求める
まず

 の場合は
の場合は が
が 桁以下になってしまうので、必ず
桁以下になってしまうので、必ず

 であるといえます。 また、
であるといえます。 また、

 の場合は
の場合は 倍すると
倍すると 桁以上になってしまうため、
桁以上になってしまうため、

 といえます。 つまり、
といえます。 つまり、 は
は か
か のどちらかとなります。
のどちらかとなります。


 の場合は
の場合は が
が 桁以下になってしまうので、必ず
桁以下になってしまうので、必ず

 であるといえます。 また、
であるといえます。 また、

 の場合は
の場合は 倍すると
倍すると 桁以上になってしまうため、
桁以上になってしまうため、

 といえます。 つまり、
といえます。 つまり、 は
は か
か のどちらかとなります。
のどちらかとなります。ここで仮に

 だとすると、方程式は「
だとすると、方程式は「


































 」となり、右辺の一の位が「
」となり、右辺の一の位が「 」になっています。 左辺は整数を
」になっています。 左辺は整数を 倍した数ですが、
倍した数ですが、 倍して一の位が
倍して一の位が になる整数はありませんので、左辺と右辺は常に一致しません。 つまり、
になる整数はありませんので、左辺と右辺は常に一致しません。 つまり、

 の場合に解は存在しないことが判ります。 よって、解が存在するとしたら
の場合に解は存在しないことが判ります。 よって、解が存在するとしたら

 の場合のみとなります。
の場合のみとなります。


 だとすると、方程式は「
だとすると、方程式は「


































 」となり、右辺の一の位が「
」となり、右辺の一の位が「 」になっています。 左辺は整数を
」になっています。 左辺は整数を 倍した数ですが、
倍した数ですが、 倍して一の位が
倍して一の位が になる整数はありませんので、左辺と右辺は常に一致しません。 つまり、
になる整数はありませんので、左辺と右辺は常に一致しません。 つまり、

 の場合に解は存在しないことが判ります。 よって、解が存在するとしたら
の場合に解は存在しないことが判ります。 よって、解が存在するとしたら

 の場合のみとなります。
の場合のみとなります。5.4dの値を求める


 を代入すると、方程式は「
を代入すると、方程式は「


































 」になります。 ここで右辺の一の位は「
」になります。 ここで右辺の一の位は「 」ですが、
」ですが、 倍して一の位が
倍して一の位が になる整数の一の位は、「
になる整数の一の位は、「




 」「
」「




 」しかありませんので、よって左辺の一の位である
」しかありませんので、よって左辺の一の位である は
は か
か となります。
となります。ここで

 だとすると、方程式は「
だとすると、方程式は「

































 」になりますが、この式を整理すると「
」になりますが、この式を整理すると「











 」になり、
」になり、 に
に ~
~ のどの値を入れても
のどの値を入れても は負の数になるため、
は負の数になるため、

 であることが判ります。 よって、解が存在するとしたら
であることが判ります。 よって、解が存在するとしたら

 の場合のみとなります。
の場合のみとなります。


 だとすると、方程式は「
だとすると、方程式は「

































 」になりますが、この式を整理すると「
」になりますが、この式を整理すると「











 」になり、
」になり、 に
に ~
~ のどの値を入れても
のどの値を入れても は負の数になるため、
は負の数になるため、

 であることが判ります。 よって、解が存在するとしたら
であることが判ります。 よって、解が存在するとしたら

 の場合のみとなります。
の場合のみとなります。5.5bとcの値を求める


 を代入すると、方程式は「
を代入すると、方程式は「

































 」になり、この式を変形すると「
」になり、この式を変形すると「









 」となります。 ここで「
」となります。 ここで「







 」が整数になるためには、
」が整数になるためには、 に
に ~
~ の数を当てはめてみると、
の数を当てはめてみると、

 だけであることが分かります。
だけであることが分かります。

 を、
を、









 に代入して、
に代入して、










 より、
より、

 です。
です。よって、

 、
、

 、
、

 、
、

 より、
より、




 です。 試しに
です。 試しに




 を計算すると、
を計算すると、


 となって、確かに「
となって、確かに「 倍するともとの数の逆順になっている」ことが分かります。
倍するともとの数の逆順になっている」ことが分かります。


 、
、

 、
、

 、
、

 より、
より、




 です。 試しに
です。 試しに




 を計算すると、
を計算すると、


 となって、確かに「
となって、確かに「 倍するともとの数の逆順になっている」ことが分かります。
倍するともとの数の逆順になっている」ことが分かります。今回は、整数の基本的な性質を紹介しました。 次回は「実数」と、これらの数を扱う上で重要となる「関数」や「写像」を説明します!