1.有理数と実数
さて、ここまで整数について扱ってきましたが、ここからはさらに細かな「有理数(ゆうりすう)」や「実数(じっすう)」を扱います。 これらは、いわゆる「小数」のことです。
1.1有理数
「整数 整数」の分数で表せる、分母が
整数」の分数で表せる、分母が 以外の数を「有理数(ゆうりすう)」といいます。 例えば、「
以外の数を「有理数(ゆうりすう)」といいます。 例えば、「

 」や「
」や「

 」や「
」や「


 」は有理数です。 「
」は有理数です。 「





 」という小数も、「
」という小数も、「


 」という分数で表せるので有理数です。
」という分数で表せるので有理数です。
 整数」の分数で表せる、分母が
整数」の分数で表せる、分母が 以外の数を「有理数(ゆうりすう)」といいます。 例えば、「
以外の数を「有理数(ゆうりすう)」といいます。 例えば、「

 」や「
」や「

 」や「
」や「


 」は有理数です。 「
」は有理数です。 「





 」という小数も、「
」という小数も、「


 」という分数で表せるので有理数です。
」という分数で表せるので有理数です。このとき、有理数全体の集合を「 」と表すことにします。 つまり、「
」と表すことにします。 つまり、「
























 」です。
」です。
 」と表すことにします。 つまり、「
」と表すことにします。 つまり、「
























 」です。
」です。1.2小数から分数への変換
ちなみに、「












 」のように数字が循環する小数は必ず「整数
」のように数字が循環する小数は必ず「整数 整数」の分数に直すことができ、有理数になります。 「
整数」の分数に直すことができ、有理数になります。 「

 」も、「
」も、「





 」と循環しているので有理数です。
」と循環しているので有理数です。













 」のように数字が循環する小数は必ず「整数
」のように数字が循環する小数は必ず「整数 整数」の分数に直すことができ、有理数になります。 「
整数」の分数に直すことができ、有理数になります。 「

 」も、「
」も、「





 」と循環しているので有理数です。
」と循環しているので有理数です。「












 」のように循環している小数を分数に直す方法は以下の通りです。
」のように循環している小数を分数に直す方法は以下の通りです。













 」のように循環している小数を分数に直す方法は以下の通りです。
」のように循環している小数を分数に直す方法は以下の通りです。














 とおく。
とおく。- 小数の循環している一周分が小数点の左に出るように、両辺に

 の累乗の数を掛ける。 つまり、
の累乗の数を掛ける。 つまり、





















 。
。 - この両辺から、















 の両辺をそれぞれ引く。 つまり、
の両辺をそれぞれ引く。 つまり、







 。
。 - 式を変形して、

















 より、
より、




















 。
。
循環する小数であればどんな小数も、この方法で分数に直せます。
1.3無理数
一方で、循環しない小数のことを、「無理数(むりすう)」といいます。 無理数は、「整数 整数」の分数で表せません。 無理数には、例えば円周率「
整数」の分数で表せません。 無理数には、例えば円周率「








 」や、
」や、 乗すると
乗すると になる数「
になる数「









 」があります。
」があります。
 整数」の分数で表せません。 無理数には、例えば円周率「
整数」の分数で表せません。 無理数には、例えば円周率「








 」や、
」や、 乗すると
乗すると になる数「
になる数「









 」があります。
」があります。そして、有理数と無理数を合わせて「実数」といいます。 実数全体の集合を「 」と表すことにします。
」と表すことにします。
 」と表すことにします。
」と表すことにします。補足
この「実数」の定義には、「小数」という曖昧なものを使ってしまいましたが、より厳密に定義することもできます。 定義の方法はいくつかありますがその1つを簡単に言うと、有理数を限りなくたくさん並べていくと何かの数に限りなく近づくことがあります。 その数は有理数ではないことがあり、それを無理数と定義します。 有理数と無理数を合わせて実数です。
さて、すべての自然数は、整数の中に含まれます。 また、すべての整数は、有理数の中に含まれます。 従って、今までに紹介した数は下記のような包含関係になります。
自然数
 整数
整数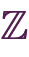
 有理数
有理数
 実数
実数
1.4主な演算
有理数および実数には、整数と同様に、2つの数

 に対して、加算「
に対して、加算「

 」、減算「
」、減算「

 」、乗算「
」、乗算「

 」、累乗「
」、累乗「
 」、絶対値「
」、絶対値「

 」が定義されています。 また
」が定義されています。 また でない
でない に対して、除算「
に対して、除算「

 」も定義されています。 ただし
」も定義されています。 ただし が
が の場合、例えば「
の場合、例えば「

 」などは未定義です。
」などは未定義です。


 に対して、加算「
に対して、加算「

 」、減算「
」、減算「

 」、乗算「
」、乗算「

 」、累乗「
」、累乗「
 」、絶対値「
」、絶対値「

 」が定義されています。 また
」が定義されています。 また でない
でない に対して、除算「
に対して、除算「

 」も定義されています。 ただし
」も定義されています。 ただし が
が の場合、例えば「
の場合、例えば「

 」などは未定義です。
」などは未定義です。さらに実数には、「平方根(へいほうこん)」が定義されます。 「 の平方根」とは、「
の平方根」とは、「

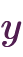
 」を満たす
」を満たす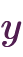 のことです。 例えば「
のことです。 例えば「 の平方根」とは、「
の平方根」とは、「


 」および「
」および「





 」が成り立つので「
」が成り立つので「


 」の2つです。 同様に、「
」の2つです。 同様に、「 の平方根」は、「
の平方根」は、「


 」です。
」です。
 の平方根」とは、「
の平方根」とは、「

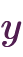
 」を満たす
」を満たす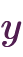 のことです。 例えば「
のことです。 例えば「 の平方根」とは、「
の平方根」とは、「


 」および「
」および「





 」が成り立つので「
」が成り立つので「


 」の2つです。 同様に、「
」の2つです。 同様に、「 の平方根」は、「
の平方根」は、「


 」です。
」です。平方根のうち正の数のほうを「正(せい)の平方根(へいほうこん)」といい「 」の記号で表します。 つまり「
」の記号で表します。 つまり「

 」「
」「

 」です。
」です。
 」の記号で表します。 つまり「
」の記号で表します。 つまり「

 」「
」「

 」です。
」です。またこれを拡張して、「

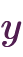
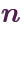 」を満たす
」を満たす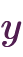 の値を「
の値を「 の
の 乗根(じょうこん)」といいます。 そして、正の
乗根(じょうこん)」といいます。 そして、正の の
の 乗根を「
乗根を「![\sqrt[n]{x}](/m/sqrt_n_x.webp) 」と表します。 例えば「
」と表します。 例えば「



 」なので、「
」なので、「![\sqrt[4]{16}](/m/sqrt_4_16.webp)

 」です。
」です。


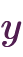
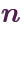 」を満たす
」を満たす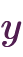 の値を「
の値を「 の
の 乗根(じょうこん)」といいます。 そして、正の
乗根(じょうこん)」といいます。 そして、正の の
の 乗根を「
乗根を「![\sqrt[n]{x}](/m/sqrt_n_x.webp) 」と表します。 例えば「
」と表します。 例えば「



 」なので、「
」なので、「![\sqrt[4]{16}](/m/sqrt_4_16.webp)

 」です。
」です。正の平方根の値をいくつか挙げると、以下のようになります。
| 正の平方根 |
|---|
   |
   |
               |
               |
   |
               |
               |
               |
               |
   |
正の平方根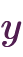

 をグラフで表示すると、下図のようになります。
をグラフで表示すると、下図のようになります。  が
が 未満の場合には、
未満の場合には、 乗して
乗して になる実数が存在しないため、
になる実数が存在しないため、 は定義されません。
は定義されません。
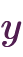

 をグラフで表示すると、下図のようになります。
をグラフで表示すると、下図のようになります。  が
が 未満の場合には、
未満の場合には、 乗して
乗して になる実数が存在しないため、
になる実数が存在しないため、 は定義されません。
は定義されません。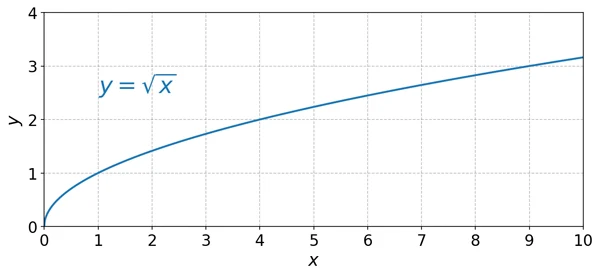
ちなみに、 は無理数になります。 簡単ですので、証明してみましょう。
は無理数になります。 簡単ですので、証明してみましょう。
 は無理数になります。 簡単ですので、証明してみましょう。
は無理数になります。 簡単ですので、証明してみましょう。- 以下では、もし
 が有理数であるなら矛盾することを示し、消去法で
が有理数であるなら矛盾することを示し、消去法で は無理数だと証明する。
は無理数だと証明する。 - まず、「
 は有理数」だと仮定する。 すると有理数の定義と、
は有理数」だと仮定する。 すると有理数の定義と、

 より、ある正の整数
より、ある正の整数

 を使って「
を使って「



 」と表せることになる。
」と表せることになる。 - 両辺を二乗して「






 」。 両辺に
」。 両辺に
 を掛けて、「
を掛けて、「




 」。
」。 

 は正の整数なので、「
は正の整数なので、「




 」の両辺とも正の整数になり、両辺はそれぞれ素因数分解が可能。 両辺をそれぞれ素因数分解すると、素因数分解の一意性により、両辺の素因数は一致するはずである。
」の両辺とも正の整数になり、両辺はそれぞれ素因数分解が可能。 両辺をそれぞれ素因数分解すると、素因数分解の一意性により、両辺の素因数は一致するはずである。

 を二乗すると、それらの素因数の個数は二倍になるため、「
を二乗すると、それらの素因数の個数は二倍になるため、「
 」と「
」と「
 」の素因数のうち
」の素因数のうち の個数はそれぞれ偶数個である。 したがって、「
の個数はそれぞれ偶数個である。 したがって、「




 」の素因数のうち
」の素因数のうち の個数は、左辺は奇数個、右辺は偶数個となり、一致せず矛盾。
の個数は、左辺は奇数個、右辺は偶数個となり、一致せず矛盾。- よって、「
 は有理数」という命題は偽になることが分かったので、排中律により、「
は有理数」という命題は偽になることが分かったので、排中律により、「 は有理数でない」という命題が真になる。 つまり、
は有理数でない」という命題が真になる。 つまり、 は無理数である。(証明終)
は無理数である。(証明終)
このように、「
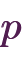 が成り立つと仮定してわざと矛盾を導き、消去法で
が成り立つと仮定してわざと矛盾を導き、消去法で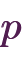 を証明する」という証明方法を「背理法(はいりほう)」といいます。
を証明する」という証明方法を「背理法(はいりほう)」といいます。

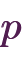 が成り立つと仮定してわざと矛盾を導き、消去法で
が成り立つと仮定してわざと矛盾を導き、消去法で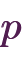 を証明する」という証明方法を「背理法(はいりほう)」といいます。
を証明する」という証明方法を「背理法(はいりほう)」といいます。2.多次方程式
2.1一次方程式
それでは、実数の方程式に挑戦してみましょう。 まずは簡単な下記の問題です。
問題





 を満たす
を満たす をすべて求めよ。
をすべて求めよ。
「




 (ただし
(ただし

 )」の形の方程式は「一次方程式(いちじほうていしき)」と呼ばれます。 一次方程式は両辺に同じ数を足したり掛けたりするだけで簡単に解けます。
)」の形の方程式は「一次方程式(いちじほうていしき)」と呼ばれます。 一次方程式は両辺に同じ数を足したり掛けたりするだけで簡単に解けます。





 (ただし
(ただし

 )」の形の方程式は「一次方程式(いちじほうていしき)」と呼ばれます。 一次方程式は両辺に同じ数を足したり掛けたりするだけで簡単に解けます。
)」の形の方程式は「一次方程式(いちじほうていしき)」と呼ばれます。 一次方程式は両辺に同じ数を足したり掛けたりするだけで簡単に解けます。




 の両辺に
の両辺に を足して、
を足して、


 。
。


 の両辺を
の両辺を で割って、
で割って、

 。
。- よって、





 を満たす
を満たす は
は 。
。
2.2二次方程式
次はやや複雑な、下記の問題です。
問題









 を満たす
を満たす をすべて求めよ。
をすべて求めよ。
「








 (ただし
(ただし

 )」の形の方程式は「二次方程式(にじほうていしき)」と呼ばれます。 二次方程式は、「
)」の形の方程式は「二次方程式(にじほうていしき)」と呼ばれます。 二次方程式は、「










 」の形に変形できれば簡単に解けるため、この形になることを目指します。
」の形に変形できれば簡単に解けるため、この形になることを目指します。









 (ただし
(ただし

 )」の形の方程式は「二次方程式(にじほうていしき)」と呼ばれます。 二次方程式は、「
)」の形の方程式は「二次方程式(にじほうていしき)」と呼ばれます。 二次方程式は、「










 」の形に変形できれば簡単に解けるため、この形になることを目指します。
」の形に変形できれば簡単に解けるため、この形になることを目指します。まず、「










 」の式の左辺を展開します。 「
」の式の左辺を展開します。 「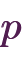






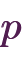


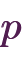
 」という規則がありますので、これを繰り返し適用して括弧を外していくと、「
」という規則がありますので、これを繰り返し適用して括弧を外していくと、「















































 」と変形できます。 問題の式に近づきました。
」と変形できます。 問題の式に近づきました。











 」の式の左辺を展開します。 「
」の式の左辺を展開します。 「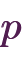






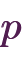


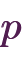
 」という規則がありますので、これを繰り返し適用して括弧を外していくと、「
」という規則がありますので、これを繰り返し適用して括弧を外していくと、「















































 」と変形できます。 問題の式に近づきました。
」と変形できます。 問題の式に近づきました。この「












 」と問題の式「
」と問題の式「








 」を見比べると、「
」を見比べると、「

 」のところに
」のところに 、「
、「
 」のところに
」のところに

 を当てはめれば、同じ式にできることが分かります。 ここで「
を当てはめれば、同じ式にできることが分かります。 ここで「



 」「
」「




 」となるような
」となるような

 を適当に考えれば「
を適当に考えれば「






 」だと分かります。 当てはめると「
」だと分かります。 当てはめると「


















 」となりました。
」となりました。













 」と問題の式「
」と問題の式「








 」を見比べると、「
」を見比べると、「

 」のところに
」のところに 、「
、「
 」のところに
」のところに

 を当てはめれば、同じ式にできることが分かります。 ここで「
を当てはめれば、同じ式にできることが分かります。 ここで「



 」「
」「




 」となるような
」となるような

 を適当に考えれば「
を適当に考えれば「






 」だと分かります。 当てはめると「
」だと分かります。 当てはめると「


















 」となりました。
」となりました。さて、ここまでの結果から、問題の式「








 」は「
」は「


















 」に変形でき、これは「
」に変形でき、これは「













 」に変形できることが分かりました。 つまり、問題の式の代わりに「
」に変形できることが分かりました。 つまり、問題の式の代わりに「










 」を満たす
」を満たす を求めればいいことになります。 するとこれは、「
を求めればいいことになります。 するとこれは、「

 」と「
」と「

 」を掛けると
」を掛けると になるという意味ですので、少なくとも一方が
になるという意味ですので、少なくとも一方が でなければなりません。
でなければなりません。









 」は「
」は「


















 」に変形でき、これは「
」に変形でき、これは「













 」に変形できることが分かりました。 つまり、問題の式の代わりに「
」に変形できることが分かりました。 つまり、問題の式の代わりに「










 」を満たす
」を満たす を求めればいいことになります。 するとこれは、「
を求めればいいことになります。 するとこれは、「

 」と「
」と「

 」を掛けると
」を掛けると になるという意味ですので、少なくとも一方が
になるという意味ですので、少なくとも一方が でなければなりません。
でなければなりません。「

 」が
」が の場合を考えると、
の場合を考えると、


 だと分かります。 「
だと分かります。 「

 」が
」が の場合を考えると、
の場合を考えると、

 だと分かります。 両方同時に
だと分かります。 両方同時に になることはありません。 よって、これらが解の全部です。 つまり
になることはありません。 よって、これらが解の全部です。 つまり








 を満たす
を満たす は、
は、




 です。
です。


 」が
」が の場合を考えると、
の場合を考えると、


 だと分かります。 「
だと分かります。 「

 」が
」が の場合を考えると、
の場合を考えると、

 だと分かります。 両方同時に
だと分かります。 両方同時に になることはありません。 よって、これらが解の全部です。 つまり
になることはありません。 よって、これらが解の全部です。 つまり








 を満たす
を満たす は、
は、




 です。
です。2.3二次方程式の解の公式
ちなみに、二次方程式の解は「二次方程式(にじほうていしき)の解(かい)の公式(こうしき)」と呼ばれる下記の式でも解けます。

確かに、先ほどと同じ解が得られました。
3.写像
さて最後に、関数と写像について解説します。
「写像(しゃぞう)」とは、ある集合のすべての元それぞれをある集合の元に対応付けるもので、「関数(かんすう)」と呼ばれることもあります。 下図における、元と元とを結ぶ「矢印」の集まりに相当するものが写像です。
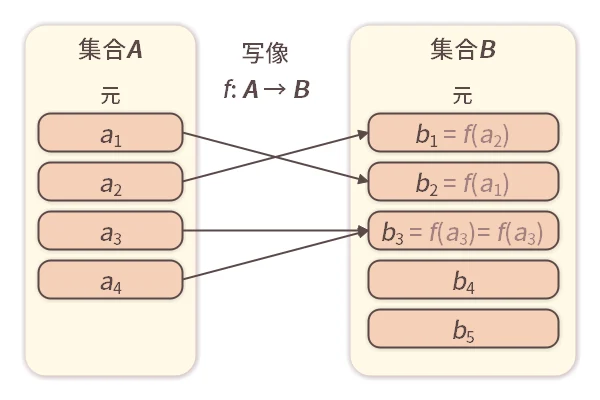
写像 が集合
が集合 の元と集合
の元と集合 の元を対応付けることを「
の元を対応付けることを「



 」と表します。 またこのとき、集合
」と表します。 またこのとき、集合 の元
の元 に対応する集合
に対応する集合 の元を「
の元を「


 」と表します。 例えばこの図では、元
」と表します。 例えばこの図では、元
 に元
に元
 が対応付いているため、
が対応付いているため、






 となります。
となります。
 が集合
が集合 の元と集合
の元と集合 の元を対応付けることを「
の元を対応付けることを「



 」と表します。 またこのとき、集合
」と表します。 またこのとき、集合 の元
の元 に対応する集合
に対応する集合 の元を「
の元を「


 」と表します。 例えばこの図では、元
」と表します。 例えばこの図では、元
 に元
に元
 が対応付いているため、
が対応付いているため、






 となります。
となります。「



 」のとき、集合
」のとき、集合 のどのような元
のどのような元 に対しても、対応する元
に対しても、対応する元


 は集合
は集合 に1つだけ存在します。 対応先が存在しなかったり、複数存在することはありません。
に1つだけ存在します。 対応先が存在しなかったり、複数存在することはありません。




 」のとき、集合
」のとき、集合 のどのような元
のどのような元 に対しても、対応する元
に対しても、対応する元


 は集合
は集合 に1つだけ存在します。 対応先が存在しなかったり、複数存在することはありません。
に1つだけ存在します。 対応先が存在しなかったり、複数存在することはありません。また写像は、同じ集合の間で対応付けることもできます。 つまり「



 」であっても構いません。
」であっても構いません。




 」であっても構いません。
」であっても構いません。例えば、自然数全体の集合 に対し、
に対し、 の元
の元 を2倍する「
を2倍する「





 」は、写像「
」は、写像「



 」となります。
」となります。
 に対し、
に対し、 の元
の元 を2倍する「
を2倍する「





 」は、写像「
」は、写像「



 」となります。
」となります。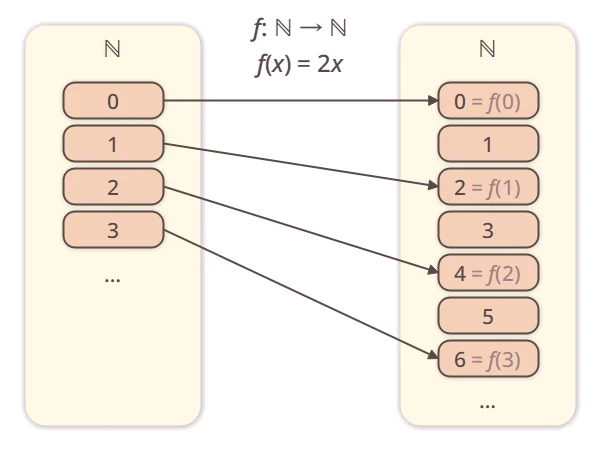
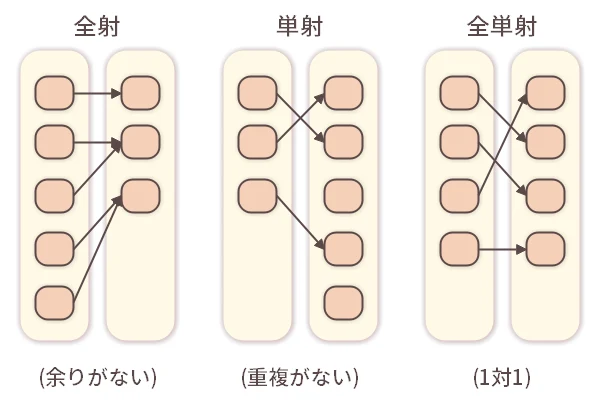
3.1全射、単射、全単射
「



 」において、
」において、 の元が
の元が のすべての元を余すところなく対応付けている場合、
のすべての元を余すところなく対応付けている場合、 を「全射(ぜんしゃ)」といいます。 厳密には、集合
を「全射(ぜんしゃ)」といいます。 厳密には、集合 のすべての元
のすべての元 に対する
に対する


 を集めたものが集合
を集めたものが集合 と一致したとき、
と一致したとき、 は全射です。
は全射です。




 」において、
」において、 の元が
の元が のすべての元を余すところなく対応付けている場合、
のすべての元を余すところなく対応付けている場合、 を「全射(ぜんしゃ)」といいます。 厳密には、集合
を「全射(ぜんしゃ)」といいます。 厳密には、集合 のすべての元
のすべての元 に対する
に対する


 を集めたものが集合
を集めたものが集合 と一致したとき、
と一致したとき、 は全射です。
は全射です。また、 のそれぞれの元に対応する
のそれぞれの元に対応する の元に重複が無いとき、
の元に重複が無いとき、 を「単射(たんしゃ)」といいます。 厳密には、
を「単射(たんしゃ)」といいます。 厳密には、 の任意の異なる2つの元
の任意の異なる2つの元

 に対し、必ず
に対し、必ず


 と
と


 が異なるとき、
が異なるとき、 は単射です。
は単射です。
 のそれぞれの元に対応する
のそれぞれの元に対応する の元に重複が無いとき、
の元に重複が無いとき、 を「単射(たんしゃ)」といいます。 厳密には、
を「単射(たんしゃ)」といいます。 厳密には、 の任意の異なる2つの元
の任意の異なる2つの元

 に対し、必ず
に対し、必ず


 と
と


 が異なるとき、
が異なるとき、 は単射です。
は単射です。写像 が全射かつ単射であるとき、
が全射かつ単射であるとき、 を「全単射(ぜんたんしゃ)」といいます。 このとき、
を「全単射(ぜんたんしゃ)」といいます。 このとき、 の元と
の元と の元がちょうど1対1で対応する形になります。
の元がちょうど1対1で対応する形になります。
 が全射かつ単射であるとき、
が全射かつ単射であるとき、 を「全単射(ぜんたんしゃ)」といいます。 このとき、
を「全単射(ぜんたんしゃ)」といいます。 このとき、 の元と
の元と の元がちょうど1対1で対応する形になります。
の元がちょうど1対1で対応する形になります。全射、単射、全単射のイメージを下図にまとめました。
3.2逆写像
写像 の、元の対応の向きを逆にした写像を、
の、元の対応の向きを逆にした写像を、 の「逆写像(ぎゃくしゃぞう)」といい「
の「逆写像(ぎゃくしゃぞう)」といい「

 」と表します。 厳密に説明するとややこしいですが、「
」と表します。 厳密に説明するとややこしいですが、「



 」「
」「



 」の2つの写像が、
」の2つの写像が、 の任意の元
の任意の元 に対して常に「
に対して常に「







 」を満たし、
」を満たし、 の任意の元
の任意の元 に対して常に「
に対して常に「







 」を満たすとき、
」を満たすとき、 は
は の逆写像「
の逆写像「



 」です。
」です。
 の、元の対応の向きを逆にした写像を、
の、元の対応の向きを逆にした写像を、 の「逆写像(ぎゃくしゃぞう)」といい「
の「逆写像(ぎゃくしゃぞう)」といい「

 」と表します。 厳密に説明するとややこしいですが、「
」と表します。 厳密に説明するとややこしいですが、「



 」「
」「



 」の2つの写像が、
」の2つの写像が、 の任意の元
の任意の元 に対して常に「
に対して常に「







 」を満たし、
」を満たし、 の任意の元
の任意の元 に対して常に「
に対して常に「







 」を満たすとき、
」を満たすとき、 は
は の逆写像「
の逆写像「



 」です。
」です。例えば、「






 」という写像「
」という写像「


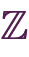 」と、「
」と、「






 」という写像「
」という写像「

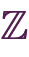

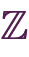 」を考えると、対応の向きが逆になっていますので
」を考えると、対応の向きが逆になっていますので は
は の逆写像「
の逆写像「



 」だといえます。
」だといえます。







 」という写像「
」という写像「

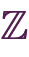

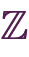 」と、「
」と、「






 」という写像「
」という写像「

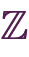

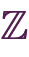 」を考えると、対応の向きが逆になっていますので
」を考えると、対応の向きが逆になっていますので は
は の逆写像「
の逆写像「



 」だといえます。
」だといえます。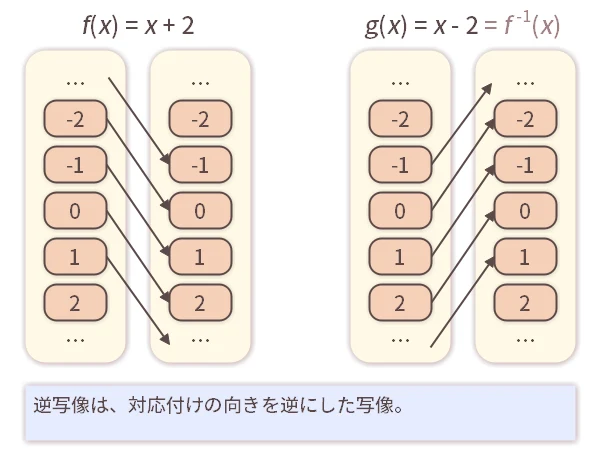
ちなみに、写像 が全単射でなければ、
が全単射でなければ、 に逆写像は存在しません。 また
に逆写像は存在しません。 また が全単射であれば、必ず
が全単射であれば、必ず の逆写像
の逆写像

 が存在し、それは1種類しかありません。
が存在し、それは1種類しかありません。
 が全単射でなければ、
が全単射でなければ、 に逆写像は存在しません。 また
に逆写像は存在しません。 また が全単射であれば、必ず
が全単射であれば、必ず の逆写像
の逆写像

 が存在し、それは1種類しかありません。
が存在し、それは1種類しかありません。今回は、実数や写像について解説しました。 次回は、三角形や円などの様々な図形について解説します!


