1.公理と定理と証明
数学では、大まかには、正しいとするいくつかの前提から出発して、正しいと言えるものを論理的に導出していきます。 これらのあらかじめ決めておいた正しい前提のことを「公理(こうり)」といいます。
そして公理の他にもいくつかのルールが定義され、数学では公理とこれらのルールを使って次々と正しいことを導出していきます。
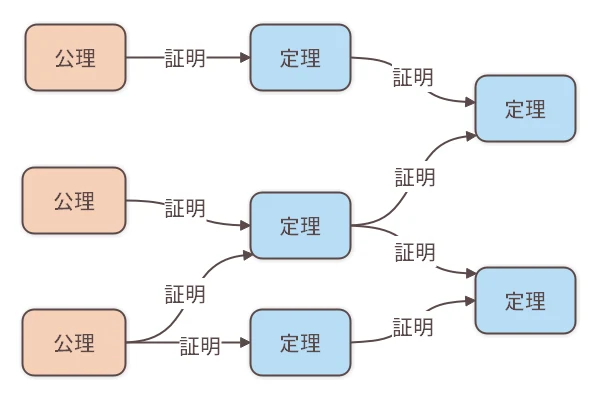
新しく導出された正しいことを、公理と合わせて「定理(ていり)」と呼び、定理を導出する過程のことを「証明(しょうめい)」といいます。
別の見方をすると、数学の問題を解くこととは、今までに導出された定理を使って、いかにその問題の答えが定理になるかという証明を見つける作業になります。
2.命題と論理式
さて、「



 である」「
である」「



 である」のような、定理であるかどうかを判断しうる対象のことを「命題(めいだい)」といいます。
である」のような、定理であるかどうかを判断しうる対象のことを「命題(めいだい)」といいます。




 である」「
である」「



 である」のような、定理であるかどうかを判断しうる対象のことを「命題(めいだい)」といいます。
である」のような、定理であるかどうかを判断しうる対象のことを「命題(めいだい)」といいます。命題の扱い方にはいくつかの方法がありますが、ここでは解りやすく論理式の「真(しん)」と「偽(ぎ)」を使って、「命題が定理であることを『真』、定理でないことを『偽』」と表すことにします。 例えば、「



 である」という命題が定理であれば、「
である」という命題が定理であれば、「



 である」は「真」です。 「
である」は「真」です。 「



 である」という命題が定理にならなければ、「
である」という命題が定理にならなければ、「



 である」は「偽」です。
である」は「偽」です。




 である」という命題が定理であれば、「
である」という命題が定理であれば、「



 である」は「真」です。 「
である」は「真」です。 「



 である」という命題が定理にならなければ、「
である」という命題が定理にならなければ、「



 である」は「偽」です。
である」は「偽」です。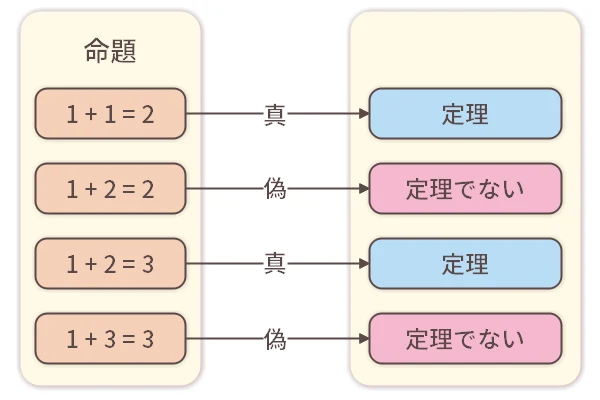
補足
このように、真と偽を扱った式のことを「論理式」と言います。 今回は、命題が定理かどうかを表すのに論理式の真偽を使うことにしましたが、命題が定理かどうかを他の方法で表すこともできます。 例えばその一つに、「トートロジー」という常に真になる命題を、定理とする考えもあります。
このとき、命題たちを「 」「
」「 」などの文字で表すことにします。 そして、「
」などの文字で表すことにします。 そして、「 ならば
ならば 」や「
」や「 かつ
かつ 」のように、これらを組み合わせて新しい命題を作ることを考えます。
」のように、これらを組み合わせて新しい命題を作ることを考えます。
 」「
」「 」などの文字で表すことにします。 そして、「
」などの文字で表すことにします。 そして、「 ならば
ならば 」や「
」や「 かつ
かつ 」のように、これらを組み合わせて新しい命題を作ることを考えます。
」のように、これらを組み合わせて新しい命題を作ることを考えます。例えば、 が「
が「



 である」という命題で、
である」という命題で、 が「
が「



 である」という命題であれば、「
である」という命題であれば、「 または
または 」とすることで、「
」とすることで、「



 である、または、
である、または、



 である」という命題が作れます。
である」という命題が作れます。
 が「
が「



 である」という命題で、
である」という命題で、 が「
が「



 である」という命題であれば、「
である」という命題であれば、「 または
または 」とすることで、「
」とすることで、「



 である、または、
である、または、



 である」という命題が作れます。
である」という命題が作れます。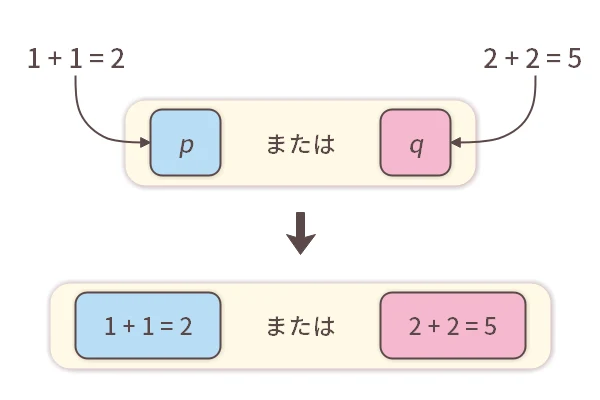
通常、「または」は「 」の記号、「かつ」は「
」の記号、「かつ」は「 」の記号で表し、「
」の記号で表し、「

 」「
」「

 」のように書きます。 つまり、「
」のように書きます。 つまり、「



 または
または



 」という命題は、「
」という命題は、「













 」と書けます。
」と書けます。
 」の記号、「かつ」は「
」の記号、「かつ」は「 」の記号で表し、「
」の記号で表し、「

 」「
」「

 」のように書きます。 つまり、「
」のように書きます。 つまり、「



 または
または



 」という命題は、「
」という命題は、「













 」と書けます。
」と書けます。ところで、「 または
または 」とは、
」とは、 か
か のどちらかが真なら真という意味です。 例えば「
のどちらかが真なら真という意味です。 例えば「



 または
または



 」という命題が真だとすると、「
」という命題が真だとすると、「



 」と「
」と「



 」のどちらか一方が真であることを意味します。 つまり「
」のどちらか一方が真であることを意味します。 つまり「

 」の結果は、次の表のようになります。
」の結果は、次の表のようになります。
 または
または 」とは、
」とは、 か
か のどちらかが真なら真という意味です。 例えば「
のどちらかが真なら真という意味です。 例えば「



 または
または



 」という命題が真だとすると、「
」という命題が真だとすると、「



 」と「
」と「



 」のどちらか一方が真であることを意味します。 つまり「
」のどちらか一方が真であることを意味します。 つまり「

 」の結果は、次の表のようになります。
」の結果は、次の表のようになります。 |
 |
   |
|---|---|---|
| 偽 | 偽 | 偽 |
| 偽 | 真 | 真 |
| 真 | 偽 | 真 |
| 真 | 真 | 真 |
一方、「 かつ
かつ 」とは、
」とは、 と
と の両方とも真なら真という意味です。 つまり「
の両方とも真なら真という意味です。 つまり「

 」の結果は、次の表のようになります。
」の結果は、次の表のようになります。
 かつ
かつ 」とは、
」とは、 と
と の両方とも真なら真という意味です。 つまり「
の両方とも真なら真という意味です。 つまり「

 」の結果は、次の表のようになります。
」の結果は、次の表のようになります。 |
 |
   |
|---|---|---|
| 偽 | 偽 | 偽 |
| 偽 | 真 | 偽 |
| 真 | 偽 | 偽 |
| 真 | 真 | 真 |
例えば「



 」が真、つまり定理であり、「
」が真、つまり定理であり、「



 」が偽、つまり定理でないとしましょう。 このとき、「
」が偽、つまり定理でないとしましょう。 このとき、「













 」は「真かつ偽」で偽となり、つまり定理ではありません。
」は「真かつ偽」で偽となり、つまり定理ではありません。




 」が真、つまり定理であり、「
」が真、つまり定理であり、「



 」が偽、つまり定理でないとしましょう。 このとき、「
」が偽、つまり定理でないとしましょう。 このとき、「













 」は「真かつ偽」で偽となり、つまり定理ではありません。
」は「真かつ偽」で偽となり、つまり定理ではありません。補足
正確には、論理式の「または」や「かつ」を使って作られた命題が真なら、それは定理であると、ここでは決めたことになります。 以降も同様に、論理式で真になるものは定理であると決めていきます。
3.論理式の性質
ここからは、定理を証明するときに必要となる、論理式のいろいろな性質について説明します。
3.1否定と排中律と矛盾
「



 である」という命題に対し、「
である」という命題に対し、「



 ではない」という否定の命題を表すときには、「
ではない」という否定の命題を表すときには、「 」の記号を使います。 命題
」の記号を使います。 命題 に対し「
に対し「 ではない」ことを「
ではない」ことを「
 」と書き、そのときの結果は次の表のようになります。
」と書き、そのときの結果は次の表のようになります。




 である」という命題に対し、「
である」という命題に対し、「



 ではない」という否定の命題を表すときには、「
ではない」という否定の命題を表すときには、「 」の記号を使います。 命題
」の記号を使います。 命題 に対し「
に対し「 ではない」ことを「
ではない」ことを「
 」と書き、そのときの結果は次の表のようになります。
」と書き、そのときの結果は次の表のようになります。 |
  |
|---|---|
| 偽 | 真 |
| 真 | 偽 |
この表から、どんな命題 であっても「
であっても「 」か「
」か「
 」のどちらか一方は真、つまり定理になることが解ります。 つまり「
」のどちらか一方は真、つまり定理になることが解ります。 つまり「 」も「
」も「
 」も定理でないような命題はありません。 この「
」も定理でないような命題はありません。 この「 も
も
 も定理にならないような命題は存在しない」という法則を「排中律(はいちゅうりつ)」といいます。
も定理にならないような命題は存在しない」という法則を「排中律(はいちゅうりつ)」といいます。
 であっても「
であっても「 」か「
」か「
 」のどちらか一方は真、つまり定理になることが解ります。 つまり「
」のどちらか一方は真、つまり定理になることが解ります。 つまり「 」も「
」も「
 」も定理でないような命題はありません。 この「
」も定理でないような命題はありません。 この「 も
も
 も定理にならないような命題は存在しない」という法則を「排中律(はいちゅうりつ)」といいます。
も定理にならないような命題は存在しない」という法則を「排中律(はいちゅうりつ)」といいます。また一方で、「 も
も
 も定理である」ことを「矛盾(むじゅん)」と言います。 この表から、矛盾を引き起こす命題は存在しないことも解ります。
も定理である」ことを「矛盾(むじゅん)」と言います。 この表から、矛盾を引き起こす命題は存在しないことも解ります。
 も
も
 も定理である」ことを「矛盾(むじゅん)」と言います。 この表から、矛盾を引き起こす命題は存在しないことも解ります。
も定理である」ことを「矛盾(むじゅん)」と言います。 この表から、矛盾を引き起こす命題は存在しないことも解ります。排中律と矛盾を組み合わせると、「 が定理であるとすると矛盾する、よって
が定理であるとすると矛盾する、よって
 が定理である」のように、わざと矛盾を引き起こすことでその否定を証明することもできます。
が定理である」のように、わざと矛盾を引き起こすことでその否定を証明することもできます。
 が定理であるとすると矛盾する、よって
が定理であるとすると矛盾する、よって
 が定理である」のように、わざと矛盾を引き起こすことでその否定を証明することもできます。
が定理である」のように、わざと矛盾を引き起こすことでその否定を証明することもできます。3.2論理包含
論理式のその他の記号として、「 ならば
ならば 」を意味する「
」を意味する「

 」があります。 これは、「
」があります。 これは、「 が成立するとき、
が成立するとき、 が成立する」という命題になります。
が成立する」という命題になります。
 ならば
ならば 」を意味する「
」を意味する「

 」があります。 これは、「
」があります。 これは、「 が成立するとき、
が成立するとき、 が成立する」という命題になります。
が成立する」という命題になります。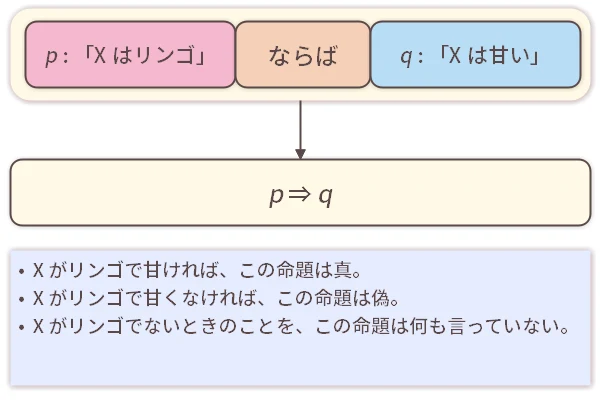
「

 」という命題が定理であることは、「
」という命題が定理であることは、「 が真」のときには常に「
が真」のときには常に「 も真」になることを意味します。
も真」になることを意味します。


 」という命題が定理であることは、「
」という命題が定理であることは、「 が真」のときには常に「
が真」のときには常に「 も真」になることを意味します。
も真」になることを意味します。このとき、「 が偽」のときには、
が偽」のときには、 はどうなっていても構いません。 つまり「
はどうなっていても構いません。 つまり「 が偽」のときには、
が偽」のときには、 が何であっても「
が何であっても「

 」が定理であることは覆らないため、このとき「
」が定理であることは覆らないため、このとき「

 」は真だといえます。
」は真だといえます。
 が偽」のときには、
が偽」のときには、 はどうなっていても構いません。 つまり「
はどうなっていても構いません。 つまり「 が偽」のときには、
が偽」のときには、 が何であっても「
が何であっても「

 」が定理であることは覆らないため、このとき「
」が定理であることは覆らないため、このとき「

 」は真だといえます。
」は真だといえます。つまり「

 」の
」の が偽の場合、
が偽の場合、 が真でも偽でも「
が真でも偽でも「

 」は真になります。 次の表のようになります。
」は真になります。 次の表のようになります。


 」の
」の が偽の場合、
が偽の場合、 が真でも偽でも「
が真でも偽でも「

 」は真になります。 次の表のようになります。
」は真になります。 次の表のようになります。 |
 |
   |
|---|---|---|
| 偽 | 偽 | 真 |
| 偽 | 真 | 真 |
| 真 | 偽 | 偽 |
| 真 | 真 | 真 |
例えば、「

 、ならば、
、ならば、 は奇数である」という定理があったとき、
は奇数である」という定理があったとき、 が
が でない場合については何も言っていないので、
でない場合については何も言っていないので、 が
が でない場合には
でない場合には が偶数でも奇数でもどうであってもこの定理が覆ることはありません。 よって、「偽、ならば、…」のときは、この命題は常に真になるべきだと理解できます。
が偶数でも奇数でもどうであってもこの定理が覆ることはありません。 よって、「偽、ならば、…」のときは、この命題は常に真になるべきだと理解できます。


 、ならば、
、ならば、 は奇数である」という定理があったとき、
は奇数である」という定理があったとき、 が
が でない場合については何も言っていないので、
でない場合については何も言っていないので、 が
が でない場合には
でない場合には が偶数でも奇数でもどうであってもこの定理が覆ることはありません。 よって、「偽、ならば、…」のときは、この命題は常に真になるべきだと理解できます。
が偶数でも奇数でもどうであってもこの定理が覆ることはありません。 よって、「偽、ならば、…」のときは、この命題は常に真になるべきだと理解できます。3.3同値な命題
さて、命題

 の真偽が常に一致するとき、
の真偽が常に一致するとき、 と
と は「同値(どうち)」といい、「
は「同値(どうち)」といい、「

 」と書きます。
」と書きます。


 の真偽が常に一致するとき、
の真偽が常に一致するとき、 と
と は「同値(どうち)」といい、「
は「同値(どうち)」といい、「

 」と書きます。
」と書きます。もし が定理のとき
が定理のとき が定理になり、そして
が定理になり、そして が定理のとき
が定理のとき が定理になるなら、それは
が定理になるなら、それは と
と は真偽が一致していると言えるため、
は真偽が一致していると言えるため、 と
と は同値です。 つまり論理式で書くと、「
は同値です。 つまり論理式で書くと、「









 」のとき、
」のとき、 と
と は同値です。 このため、「
は同値です。 このため、「

 」は「
」は「

 」という記号で書かれることもあります。
」という記号で書かれることもあります。
 が定理のとき
が定理のとき が定理になり、そして
が定理になり、そして が定理のとき
が定理のとき が定理になるなら、それは
が定理になるなら、それは と
と は真偽が一致していると言えるため、
は真偽が一致していると言えるため、 と
と は同値です。 つまり論理式で書くと、「
は同値です。 つまり論理式で書くと、「









 」のとき、
」のとき、 と
と は同値です。 このため、「
は同値です。 このため、「

 」は「
」は「

 」という記号で書かれることもあります。
」という記号で書かれることもあります。 と
と が同値なら、どちらかを証明しただけで、もう一方も証明したことになります。 「
が同値なら、どちらかを証明しただけで、もう一方も証明したことになります。 「

 」の結果は、次の表のようになります。
」の結果は、次の表のようになります。 |
 |
   |
|---|---|---|
| 偽 | 偽 | 真 |
| 偽 | 真 | 偽 |
| 真 | 偽 | 偽 |
| 真 | 真 | 真 |
3.4逆と裏と対偶
「

 」という形の命題があったとき、
」という形の命題があったとき、 と
と を反対にした「
を反対にした「

 」を「逆(ぎゃく)」の命題といいます。 また、
」を「逆(ぎゃく)」の命題といいます。 また、 と
と に否定を付けた「
に否定を付けた「







 」を「裏(うら)」といい、逆と裏の両方になった「
」を「裏(うら)」といい、逆と裏の両方になった「







 」を「対偶(たいぐう)」といいます。
」を「対偶(たいぐう)」といいます。


 」という形の命題があったとき、
」という形の命題があったとき、 と
と を反対にした「
を反対にした「

 」を「逆(ぎゃく)」の命題といいます。 また、
」を「逆(ぎゃく)」の命題といいます。 また、 と
と に否定を付けた「
に否定を付けた「







 」を「裏(うら)」といい、逆と裏の両方になった「
」を「裏(うら)」といい、逆と裏の両方になった「







 」を「対偶(たいぐう)」といいます。
」を「対偶(たいぐう)」といいます。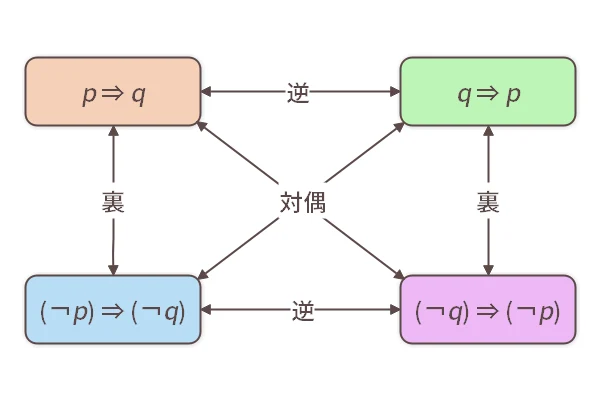
このうち特に対偶が重要で、対偶は元の命題と同値となります。 例えば「

 、ならば、
、ならば、 は奇数である」という命題に対し、対偶は「
は奇数である」という命題に対し、対偶は「 は奇数でない、ならば、
は奇数でない、ならば、

 でない」ですが、この2つの命題は同値となります。
でない」ですが、この2つの命題は同値となります。


 、ならば、
、ならば、 は奇数である」という命題に対し、対偶は「
は奇数である」という命題に対し、対偶は「 は奇数でない、ならば、
は奇数でない、ならば、

 でない」ですが、この2つの命題は同値となります。
でない」ですが、この2つの命題は同値となります。つまり命題を証明したいとき、元の命題を証明せずに対偶のほうの命題を証明することで、元の命題の証明ができます。
3.5ド・モルガンの法則
また重要な法則として、「ド・モルガンの法則(ほうそく)」があります。
ド・モルガンの法則とは、「




 」と「
」と「







 」が同値になり、「
」が同値になり、「




 」と「
」と「







 」が同値になるという法則です。 かみ砕くと、「
」が同値になるという法則です。 かみ砕くと、「


 」の括弧を外したときに、中身の「
」の括弧を外したときに、中身の「 」と「
」と「 」が入れ替わり、「
」が入れ替わり、「 」が分配されるという法則です。
」が分配されるという法則です。





 」と「
」と「







 」が同値になり、「
」が同値になり、「




 」と「
」と「







 」が同値になるという法則です。 かみ砕くと、「
」が同値になるという法則です。 かみ砕くと、「


 」の括弧を外したときに、中身の「
」の括弧を外したときに、中身の「 」と「
」と「 」が入れ替わり、「
」が入れ替わり、「 」が分配されるという法則です。
」が分配されるという法則です。例えば、「『 は偶数かつ
は偶数かつ は
は
 以上』でない」という命題は、「
以上』でない」という命題は、「 は偶数でないか、
は偶数でないか、 は
は
 以上でない」ということと同じになります。 また、「『
以上でない」ということと同じになります。 また、「『 は偶数または
は偶数または は
は
 以上』でない」ということは「
以上』でない」ということは「 は偶数でなく、
は偶数でなく、 は
は
 以上でもない」ということと同じになります。
以上でもない」ということと同じになります。
 は偶数かつ
は偶数かつ は
は
 以上』でない」という命題は、「
以上』でない」という命題は、「 は偶数でないか、
は偶数でないか、 は
は
 以上でない」ということと同じになります。 また、「『
以上でない」ということと同じになります。 また、「『 は偶数または
は偶数または は
は
 以上』でない」ということは「
以上』でない」ということは「 は偶数でなく、
は偶数でなく、 は
は
 以上でもない」ということと同じになります。
以上でもない」ということと同じになります。複雑な命題を変形して整理したいときに役立ちます。
4.命題関数
より多彩な定理や命題を扱うために、もう少し論理式について踏み込んでいきましょう。
外から値を受け取ると命題になるものを「命題関数(めいだいかんすう)」といいます。 例えば「



 である」という記述に対し、
である」という記述に対し、 に
に 、
、 に
に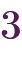 を代入すると「
を代入すると「

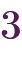

 である」という命題になりますので、「
である」という命題になりますので、「



 である」は命題関数です。
である」は命題関数です。




 である」という記述に対し、
である」という記述に対し、 に
に 、
、 に
に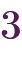 を代入すると「
を代入すると「


 である」という命題になりますので、「
である」という命題になりますので、「



 である」は命題関数です。
である」は命題関数です。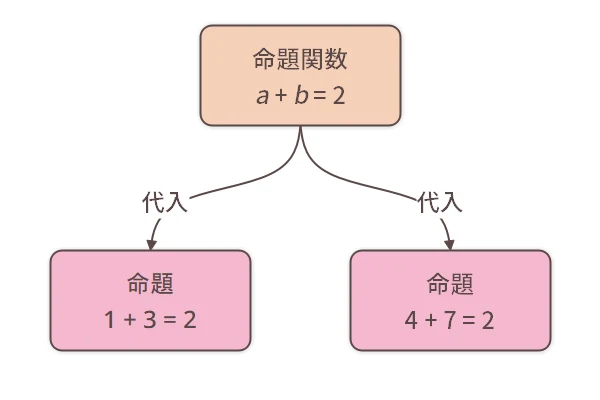
命題関数には「 」「
」「 」などの具体的な値の他に、「すべての値」や「ある値」というものを入れることができます。 これらは「
」などの具体的な値の他に、「すべての値」や「ある値」というものを入れることができます。 これらは「 」「
」「 」などの文字の前に「
」などの文字の前に「 」「
」「 」の記号を付けることで、それぞれ「すべての値」「ある値が存在する」を表します。
」の記号を付けることで、それぞれ「すべての値」「ある値が存在する」を表します。
 」「
」「 」などの具体的な値の他に、「すべての値」や「ある値」というものを入れることができます。 これらは「
」などの具体的な値の他に、「すべての値」や「ある値」というものを入れることができます。 これらは「 」「
」「 」などの文字の前に「
」などの文字の前に「 」「
」「 」の記号を付けることで、それぞれ「すべての値」「ある値が存在する」を表します。
」の記号を付けることで、それぞれ「すべての値」「ある値が存在する」を表します。例えば、「

 である」という命題関数に、
である」という命題関数に、
 で囲んで
で囲んで に
に を代入して「
を代入して「




 である
である 」のように書くと、「すべての値
」のように書くと、「すべての値 に対して
に対して

 である」という命題を表します。 同様に、
である」という命題を表します。 同様に、
 で囲んで
で囲んで に
に を代入して「
を代入して「




 である
である 」のように書くと、「
」のように書くと、「

 であるようなある値
であるようなある値 が存在する」という命題になります。
が存在する」という命題になります。


 である」という命題関数に、
である」という命題関数に、
 で囲んで
で囲んで に
に を代入して「
を代入して「




 である
である 」のように書くと、「すべての値
」のように書くと、「すべての値 に対して
に対して

 である」という命題を表します。 同様に、
である」という命題を表します。 同様に、
 で囲んで
で囲んで に
に を代入して「
を代入して「




 である
である 」のように書くと、「
」のように書くと、「

 であるようなある値
であるようなある値 が存在する」という命題になります。
が存在する」という命題になります。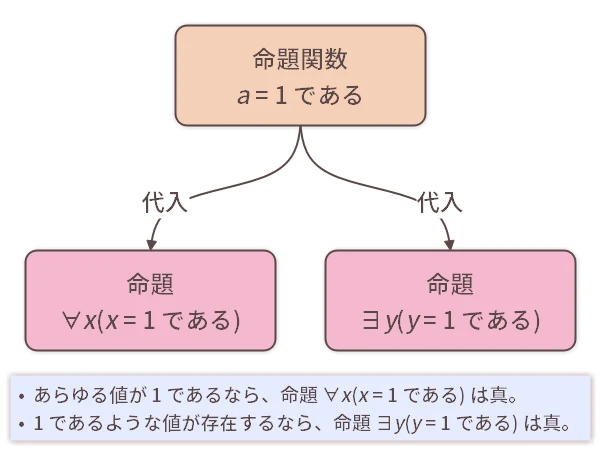
具体例として、「



 」という命題関数があり、
」という命題関数があり、 と
と に
に を入れた命題「
を入れた命題「



 」は真で、
」は真で、 に
に を
を に
に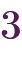 を入れた命題「
を入れた命題「

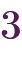

 」は偽であるとしましょう。
」は偽であるとしましょう。




 」という命題関数があり、
」という命題関数があり、 と
と に
に を入れた命題「
を入れた命題「



 」は真で、
」は真で、 に
に を
を に
に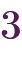 を入れた命題「
を入れた命題「

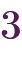

 」は偽であるとしましょう。
」は偽であるとしましょう。このとき「

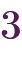

 」があるため、すべての
」があるため、すべての と
と に対して「
に対して「



 」が真になるわけではありません。 よって「
」が真になるわけではありません。 よって「











 」は偽となります。 また「
」は偽となります。 また「



 」があるため、「
」があるため、「



 」が真になるような
」が真になるような と
と は少なくとも存在しています。 よって「
は少なくとも存在しています。 よって「











 」は真となります。
」は真となります。


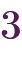

 」があるため、すべての
」があるため、すべての と
と に対して「
に対して「



 」が真になるわけではありません。 よって「
」が真になるわけではありません。 よって「











 」は偽となります。 また「
」は偽となります。 また「



 」があるため、「
」があるため、「



 」が真になるような
」が真になるような と
と は少なくとも存在しています。 よって「
は少なくとも存在しています。 よって「











 」は真となります。
」は真となります。5.直観主義論理
最後に、「直観主義論理(ちょっかんしゅぎろんり)」と呼ばれる、これまでとは異なる考え方を簡単に紹介しておきます。
これまでは、命題 と
と
 があったときに少なくとも一方は定理であるとする「排中律」を前提としていましたが、直観主義論理ではこの排中律を使いません。 つまり、「あなたは数学が好きかどうかは判らないが、あなたは数学が好きか好きでないかのどちらかだ」とこれまでの論理では言えましたが、直観主義論理ではこれすらも言えず、「あなたは数学が好きか好きでないかのどちらかである、かどうかも判らない」となります。 証明できるかどうか判らないという可能性を考慮しています。
があったときに少なくとも一方は定理であるとする「排中律」を前提としていましたが、直観主義論理ではこの排中律を使いません。 つまり、「あなたは数学が好きかどうかは判らないが、あなたは数学が好きか好きでないかのどちらかだ」とこれまでの論理では言えましたが、直観主義論理ではこれすらも言えず、「あなたは数学が好きか好きでないかのどちらかである、かどうかも判らない」となります。 証明できるかどうか判らないという可能性を考慮しています。
 と
と
 があったときに少なくとも一方は定理であるとする「排中律」を前提としていましたが、直観主義論理ではこの排中律を使いません。 つまり、「あなたは数学が好きかどうかは判らないが、あなたは数学が好きか好きでないかのどちらかだ」とこれまでの論理では言えましたが、直観主義論理ではこれすらも言えず、「あなたは数学が好きか好きでないかのどちらかである、かどうかも判らない」となります。 証明できるかどうか判らないという可能性を考慮しています。
があったときに少なくとも一方は定理であるとする「排中律」を前提としていましたが、直観主義論理ではこの排中律を使いません。 つまり、「あなたは数学が好きかどうかは判らないが、あなたは数学が好きか好きでないかのどちらかだ」とこれまでの論理では言えましたが、直観主義論理ではこれすらも言えず、「あなたは数学が好きか好きでないかのどちらかである、かどうかも判らない」となります。 証明できるかどうか判らないという可能性を考慮しています。排中律を前提にしないと、多くの定理が証明できなくなってしまうため、数学の多くの分野では直観主義論理は主流ではありませんが、論理自体を対象とする分野や計算機科学などでは直観主義論理との親和性が高くよく使われます。
今回は、数学の基本的なルールを説明しました。 次回は実際に、具体的な公理から定理を証明してみましょう!


