第1話では、数学の基本的なルールを解説しました。
今回は具体的な公理から「



 」を証明していきます。 が、その前に数学の最も基本的な要素である「集合(しゅうごう)」について説明しておこうと思います。 数学では基本的に、「
」を証明していきます。 が、その前に数学の最も基本的な要素である「集合(しゅうごう)」について説明しておこうと思います。 数学では基本的に、「



 」という数をはじめ、ほとんどのものが「集合」でできていると考えます。
」という数をはじめ、ほとんどのものが「集合」でできていると考えます。




 」を証明していきます。 が、その前に数学の最も基本的な要素である「集合(しゅうごう)」について説明しておこうと思います。 数学では基本的に、「
」を証明していきます。 が、その前に数学の最も基本的な要素である「集合(しゅうごう)」について説明しておこうと思います。 数学では基本的に、「



 」という数をはじめ、ほとんどのものが「集合」でできていると考えます。
」という数をはじめ、ほとんどのものが「集合」でできていると考えます。1.素朴集合論
1.1集合と元
「集合」とは、「いくつかのものを集めたもの」です。 「いくつかのもの」とは曖昧ですが、歴史的にも集合はこのような曖昧な捉え方から始まりました。 最終的には厳密に定義されます。
また、この「いくつかのもの」のことを「元(げん)」と呼びます。 そして、集合 の中に元
の中に元 があるとき、元
があるとき、元 は集合
は集合 に「属(ぞく)する」といい「
に「属(ぞく)する」といい「

 」と書きます。
」と書きます。
 の中に元
の中に元 があるとき、元
があるとき、元 は集合
は集合 に「属(ぞく)する」といい「
に「属(ぞく)する」といい「

 」と書きます。
」と書きます。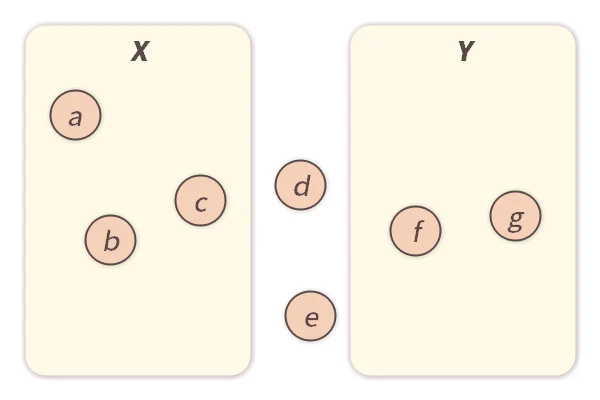
この図では、元 は集合
は集合 に属しているため、「
に属しているため、「

 」です。 一方、元
」です。 一方、元 や元
や元 は集合
は集合 に属していませんが、このように属していない場合には「
に属していませんが、このように属していない場合には「
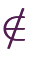
 」「
」「
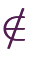
 」と書きます。
」と書きます。
 は集合
は集合 に属しているため、「
に属しているため、「

 」です。 一方、元
」です。 一方、元 や元
や元 は集合
は集合 に属していませんが、このように属していない場合には「
に属していませんが、このように属していない場合には「
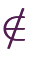
 」「
」「
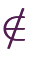
 」と書きます。
」と書きます。1.2外延的記法と内包的記法
集合にどのような元が属しているかを表すには2種類の方法があります。 「外延的記法(がいえんてききほう)」と「内包的記法(ないほうてききほう)」です。
「外延的記法」とは、集合に属する元を列挙する方法です。 例えば、集合 に「イヌ」「ネコ」「ウサギ」の元が属しているとき、外延的記法では「
に「イヌ」「ネコ」「ウサギ」の元が属しているとき、外延的記法では「

 イヌ
イヌ ネコ
ネコ ウサギ
ウサギ 」と書きます。
」と書きます。
 に「イヌ」「ネコ」「ウサギ」の元が属しているとき、外延的記法では「
に「イヌ」「ネコ」「ウサギ」の元が属しているとき、外延的記法では「

 イヌ
イヌ ネコ
ネコ ウサギ
ウサギ 」と書きます。
」と書きます。「内包的記法」とは、元の性質を記す方法です。 例えば、集合 にはすべての動物が属しているとき、内包的記法では「
にはすべての動物が属しているとき、内包的記法では「




 は動物
は動物 」と書きます。 ここでは
」と書きます。 ここでは という記号を使いましたが、好きな記号を使って「
という記号を使いましたが、好きな記号を使って「 記号
記号 記号を用いた条件文
記号を用いた条件文 」と書け、その条件を満たすものをすべて集めた集合という意味になります。
」と書け、その条件を満たすものをすべて集めた集合という意味になります。
 にはすべての動物が属しているとき、内包的記法では「
にはすべての動物が属しているとき、内包的記法では「




 は動物
は動物 」と書きます。 ここでは
」と書きます。 ここでは という記号を使いましたが、好きな記号を使って「
という記号を使いましたが、好きな記号を使って「 記号
記号 記号を用いた条件文
記号を用いた条件文 」と書け、その条件を満たすものをすべて集めた集合という意味になります。
」と書け、その条件を満たすものをすべて集めた集合という意味になります。外延的記法と内包的記法はどちらを使ってもよく、簡潔に表せるほうが使われます。
1.3含まれると等しい
次に、集合同士の関係について説明します。 例えば「

 イヌ
イヌ ネコ
ネコ ウサギ
ウサギ 」「
」「

 イヌ
イヌ ネコ
ネコ 」であるとき、
」であるとき、 の元はすべて
の元はすべて の元になっています。 このとき、集合
の元になっています。 このとき、集合 は集合
は集合 に「含(ふく)まれる」といい「
に「含(ふく)まれる」といい「

 」と書きます。
」と書きます。


 イヌ
イヌ ネコ
ネコ ウサギ
ウサギ 」「
」「

 イヌ
イヌ ネコ
ネコ 」であるとき、
」であるとき、 の元はすべて
の元はすべて の元になっています。 このとき、集合
の元になっています。 このとき、集合 は集合
は集合 に「含(ふく)まれる」といい「
に「含(ふく)まれる」といい「

 」と書きます。
」と書きます。「属する( )」と「含まれる(
)」と「含まれる( )」は記号も意味も似ていますが、混同しないように注意が必要です。 「属する」は元と集合の関係、「含まれる」は集合同士の関係です。
)」は記号も意味も似ていますが、混同しないように注意が必要です。 「属する」は元と集合の関係、「含まれる」は集合同士の関係です。
 )」と「含まれる(
)」と「含まれる( )」は記号も意味も似ていますが、混同しないように注意が必要です。 「属する」は元と集合の関係、「含まれる」は集合同士の関係です。
)」は記号も意味も似ていますが、混同しないように注意が必要です。 「属する」は元と集合の関係、「含まれる」は集合同士の関係です。補足
現代数学ではほとんどのものが集合で扱われるため、一般に集合の元も集合となり、「属する」と「含まれる」の区別はややこしいです。 「集合Xに集合Yが属する」とは、集合Xの元のどれかに集合Yがあることを表し、「集合Xに集合Yが含まれる」とは、集合Xの元に集合Yのすべての元が現れることを表します。
また、集合 と集合
と集合 の元がすべて一致しているとき、集合
の元がすべて一致しているとき、集合 と集合
と集合 は「等(ひと)しい」といい、「
は「等(ひと)しい」といい、「

 」と書きます。 等しくない場合は「
」と書きます。 等しくない場合は「

 」と書きます。 集合の元の並びには順番はなく、また元が重複したときは1つとみなします。 つまり、「
」と書きます。 集合の元の並びには順番はなく、また元が重複したときは1つとみなします。 つまり、「

 イヌ
イヌ ネコ
ネコ ウサギ
ウサギ 」「
」「

 ウサギ
ウサギ ネコ
ネコ イヌ
イヌ イヌ
イヌ イヌ
イヌ 」のとき、「
」のとき、「

 」は成り立ちます。
」は成り立ちます。
 と集合
と集合 の元がすべて一致しているとき、集合
の元がすべて一致しているとき、集合 と集合
と集合 は「等(ひと)しい」といい、「
は「等(ひと)しい」といい、「

 」と書きます。 等しくない場合は「
」と書きます。 等しくない場合は「

 」と書きます。 集合の元の並びには順番はなく、また元が重複したときは1つとみなします。 つまり、「
」と書きます。 集合の元の並びには順番はなく、また元が重複したときは1つとみなします。 つまり、「

 イヌ
イヌ ネコ
ネコ ウサギ
ウサギ 」「
」「

 ウサギ
ウサギ ネコ
ネコ イヌ
イヌ イヌ
イヌ イヌ
イヌ 」のとき、「
」のとき、「

 」は成り立ちます。
」は成り立ちます。「 」「
」「 」の記号は、元同士の比較の際にも使われます。 元
」の記号は、元同士の比較の際にも使われます。 元 と元
と元 が同じものであれば「
が同じものであれば「

 」、異なれば「
」、異なれば「

 」と書かれます。
」と書かれます。
 」「
」「 」の記号は、元同士の比較の際にも使われます。 元
」の記号は、元同士の比較の際にも使われます。 元 と元
と元 が同じものであれば「
が同じものであれば「

 」、異なれば「
」、異なれば「

 」と書かれます。
」と書かれます。1.4集合の集合
さて、「ある集合を元とする集合」というものも考えることができます。 例えば、「イヌ」を元とする集合は「 イヌ
イヌ 」となりますが、この集合を元とする集合は「
」となりますが、この集合を元とする集合は「
 イヌ
イヌ
 」となります。
」となります。
 イヌ
イヌ 」となりますが、この集合を元とする集合は「
」となりますが、この集合を元とする集合は「
 イヌ
イヌ
 」となります。
」となります。例えば、「集合


 イヌ
イヌ

 ネコ
ネコ
 」「集合
」「集合


 イヌ
イヌ
 」「集合
」「集合

 イヌ
イヌ 」であるとき、「
」であるとき、「

 」「
」「

 」です。 元と集合の関係なのか、集合同士の関係なのかに注意してください。
」です。 元と集合の関係なのか、集合同士の関係なのかに注意してください。



 イヌ
イヌ

 ネコ
ネコ
 」「集合
」「集合


 イヌ
イヌ
 」「集合
」「集合

 イヌ
イヌ 」であるとき、「
」であるとき、「

 」「
」「

 」です。 元と集合の関係なのか、集合同士の関係なのかに注意してください。
」です。 元と集合の関係なのか、集合同士の関係なのかに注意してください。1.5和集合と共通部分
第1話の命題の説明で「または( )」と「かつ(
)」と「かつ( )」を解説しましたが、集合にもこれと似たものが用意されています。 集合では「または」は「
)」を解説しましたが、集合にもこれと似たものが用意されています。 集合では「または」は「 」の記号、「かつ」は「
」の記号、「かつ」は「 」の記号で表し、集合
」の記号で表し、集合 、
、 に対して「
に対して「

 」「
」「

 」のように書きます。
」のように書きます。
 )」と「かつ(
)」と「かつ( )」を解説しましたが、集合にもこれと似たものが用意されています。 集合では「または」は「
)」を解説しましたが、集合にもこれと似たものが用意されています。 集合では「または」は「 」の記号、「かつ」は「
」の記号、「かつ」は「 」の記号で表し、集合
」の記号で表し、集合 、
、 に対して「
に対して「

 」「
」「

 」のように書きます。
」のように書きます。例えば、「甘いもの」を集めた集合 が「
が「

 ハチミツ
ハチミツ 砂糖
砂糖 グレープフルーツ
グレープフルーツ 」と定義され、「酸っぱいもの」を集めた集合
」と定義され、「酸っぱいもの」を集めた集合 が「
が「

 酢
酢 レモン
レモン グレープフルーツ
グレープフルーツ 」と定義されているとしましょう。 このとき、「甘いもの、または、酸っぱいもの」は「
」と定義されているとしましょう。 このとき、「甘いもの、または、酸っぱいもの」は「



 ハチミツ
ハチミツ 砂糖
砂糖 グレープフルーツ
グレープフルーツ 酢
酢 レモン
レモン 」となり、「甘いもの、かつ、酸っぱいもの」は「
」となり、「甘いもの、かつ、酸っぱいもの」は「



 グレープフルーツ
グレープフルーツ 」となります。
」となります。
 が「
が「

 ハチミツ
ハチミツ 砂糖
砂糖 グレープフルーツ
グレープフルーツ 」と定義され、「酸っぱいもの」を集めた集合
」と定義され、「酸っぱいもの」を集めた集合 が「
が「

 酢
酢 レモン
レモン グレープフルーツ
グレープフルーツ 」と定義されているとしましょう。 このとき、「甘いもの、または、酸っぱいもの」は「
」と定義されているとしましょう。 このとき、「甘いもの、または、酸っぱいもの」は「



 ハチミツ
ハチミツ 砂糖
砂糖 グレープフルーツ
グレープフルーツ 酢
酢 レモン
レモン 」となり、「甘いもの、かつ、酸っぱいもの」は「
」となり、「甘いもの、かつ、酸っぱいもの」は「



 グレープフルーツ
グレープフルーツ 」となります。
」となります。つまり、「 」とは集合を結合させるもので、「
」とは集合を結合させるもので、「 」とは集合の共通部分を抜き出すものと言えます。
」とは集合の共通部分を抜き出すものと言えます。
 」とは集合を結合させるもので、「
」とは集合を結合させるもので、「 」とは集合の共通部分を抜き出すものと言えます。
」とは集合の共通部分を抜き出すものと言えます。1.6空集合
1つも元が存在しない集合を「空集合(くうしゅうごう)」といい、「 」の記号で表します。 例えば、集合
」の記号で表します。 例えば、集合 に元が1つもないとき「
に元が1つもないとき「

 」です。 この記号はギリシャ文字の「
」です。 この記号はギリシャ文字の「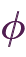 (ファイ)」に似ていますが、別記号です。
(ファイ)」に似ていますが、別記号です。
 」の記号で表します。 例えば、集合
」の記号で表します。 例えば、集合 に元が1つもないとき「
に元が1つもないとき「

 」です。 この記号はギリシャ文字の「
」です。 この記号はギリシャ文字の「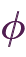 (ファイ)」に似ていますが、別記号です。
(ファイ)」に似ていますが、別記号です。「 」と「
」と「

 」は異なる集合です。 「
」は異なる集合です。 「 」は元が1つもない集合ですが、「
」は元が1つもない集合ですが、「

 」は「
」は「 」を元とする集合です。
」を元とする集合です。
 」と「
」と「

 」は異なる集合です。 「
」は異なる集合です。 「 」は元が1つもない集合ですが、「
」は元が1つもない集合ですが、「

 」は「
」は「 」を元とする集合です。
」を元とする集合です。2.自然数
さて、それでは「



 」を証明するために、集合を使って「自然数」を定義しましょう。
」を証明するために、集合を使って「自然数」を定義しましょう。




 」を証明するために、集合を使って「自然数」を定義しましょう。
」を証明するために、集合を使って「自然数」を定義しましょう。「自然数(しぜんすう)」とは「









 」と延々と続く一連の数のことです。 「
」と延々と続く一連の数のことです。 「 」を自然数に含めるかどうかは流派によって異なります。 現代数学では含めることが多いですが、数論の分野では「ただし
」を自然数に含めるかどうかは流派によって異なります。 現代数学では含めることが多いですが、数論の分野では「ただし は除く」という但し書きが頻出することになるので含めない場合も多いです。 今回は含めることにします。
は除く」という但し書きが頻出することになるので含めない場合も多いです。 今回は含めることにします。










 」と延々と続く一連の数のことです。 「
」と延々と続く一連の数のことです。 「 」を自然数に含めるかどうかは流派によって異なります。 現代数学では含めることが多いですが、数論の分野では「ただし
」を自然数に含めるかどうかは流派によって異なります。 現代数学では含めることが多いですが、数論の分野では「ただし は除く」という但し書きが頻出することになるので含めない場合も多いです。 今回は含めることにします。
は除く」という但し書きが頻出することになるので含めない場合も多いです。 今回は含めることにします。自然数全体の集合 を定義してみましょう。
を定義してみましょう。  の定義は、例えば「
の定義は、例えば「













 」などとすれば十分に思えるかもしれません。 しかしこれは、次に「
」などとすれば十分に思えるかもしれません。 しかしこれは、次に「





 」と続くことをわたしたちが知っているという前提の上に成り立っていますので、厳密な定義とは言えません。 そこで今回は、自然数の定義として「ペアノの公理(こうり)」と呼ばれるものを採用することにします。
」と続くことをわたしたちが知っているという前提の上に成り立っていますので、厳密な定義とは言えません。 そこで今回は、自然数の定義として「ペアノの公理(こうり)」と呼ばれるものを採用することにします。
 を定義してみましょう。
を定義してみましょう。  の定義は、例えば「
の定義は、例えば「













 」などとすれば十分に思えるかもしれません。 しかしこれは、次に「
」などとすれば十分に思えるかもしれません。 しかしこれは、次に「





 」と続くことをわたしたちが知っているという前提の上に成り立っていますので、厳密な定義とは言えません。 そこで今回は、自然数の定義として「ペアノの公理(こうり)」と呼ばれるものを採用することにします。
」と続くことをわたしたちが知っているという前提の上に成り立っていますので、厳密な定義とは言えません。 そこで今回は、自然数の定義として「ペアノの公理(こうり)」と呼ばれるものを採用することにします。「ペアノの公理」によると、「自然数」とは下記の構造を満たすものをいいます。
- 「
 」は自然数である。
」は自然数である。 - 「
 」が自然数ならば、「
」が自然数ならば、「 の次の数」も自然数である。
の次の数」も自然数である。 - 「
 」と「
」と「 」が等しい自然数であるとき、かつそのときに限って、「
」が等しい自然数であるとき、かつそのときに限って、「 の次の数」と「
の次の数」と「 の次の数」は等しい自然数である。
の次の数」は等しい自然数である。 - 「次の数」が「
 」であるような自然数は存在しない。
」であるような自然数は存在しない。 - 以上で定めたものだけが自然数である。
噛み砕くと、「 」から出発して、「
」から出発して、「 の次の数は
の次の数は 」「
」「 の次の数は
の次の数は 」のように延々と連ねて、分かれ道やループが無いものを「自然数」と言っています。 この定義の(1)から(5)の内容を図示すると、下記のようになります。
」のように延々と連ねて、分かれ道やループが無いものを「自然数」と言っています。 この定義の(1)から(5)の内容を図示すると、下記のようになります。
 」から出発して、「
」から出発して、「 の次の数は
の次の数は 」「
」「 の次の数は
の次の数は 」のように延々と連ねて、分かれ道やループが無いものを「自然数」と言っています。 この定義の(1)から(5)の内容を図示すると、下記のようになります。
」のように延々と連ねて、分かれ道やループが無いものを「自然数」と言っています。 この定義の(1)から(5)の内容を図示すると、下記のようになります。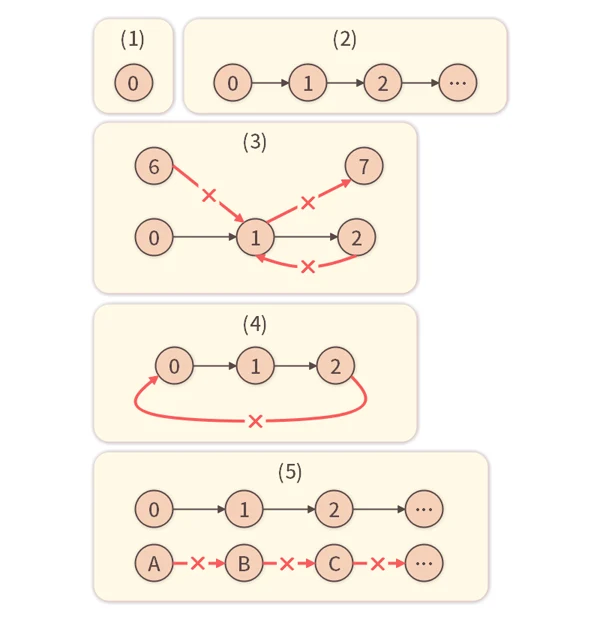
(3)や(4)では分かれ道やループをなくし、(5)では「





 」以外の列をなくしています。 この図から、自然数が「
」以外の列をなくしています。 この図から、自然数が「







 」と一本道になるように、それ以外のケースを排除していることが分かります。
」と一本道になるように、それ以外のケースを排除していることが分かります。






 」以外の列をなくしています。 この図から、自然数が「
」以外の列をなくしています。 この図から、自然数が「







 」と一本道になるように、それ以外のケースを排除していることが分かります。
」と一本道になるように、それ以外のケースを排除していることが分かります。さて、このような「構造」を満たすものはすべて自然数と見なすことにします。 重要な点は、「自然数」というものが具体的に存在するのではなく、具体的な何かがこのような「構造」になっているときにそれを自然数と呼ぶことです。 こう捉えることで、様々なものを自然数として扱うことができます。
それでは、集合だけを使って自然数を構築してみましょう。 冒頭で説明した通り、集合は数学の基本的な要素ですので、集合だけで自然数の構造が構築できれば、自然数も数学の要素として扱えるようになります。
例えば、 を空集合「
を空集合「 」で表し、数
」で表し、数 に対して次の数を「
に対して次の数を「

 」で表すと、「
」で表すと、「

 」「
」「



 」「
」「





 」「
」「







 」「
」「









 」としていくことで「
」としていくことで「









 」が定義できます。 これはペアノの公理の各条件を満たしています。 よってこれは自然数であると言えます。
」が定義できます。 これはペアノの公理の各条件を満たしています。 よってこれは自然数であると言えます。
 を空集合「
を空集合「 」で表し、数
」で表し、数 に対して次の数を「
に対して次の数を「

 」で表すと、「
」で表すと、「

 」「
」「



 」「
」「





 」「
」「







 」「
」「









 」としていくことで「
」としていくことで「









 」が定義できます。 これはペアノの公理の各条件を満たしています。 よってこれは自然数であると言えます。
」が定義できます。 これはペアノの公理の各条件を満たしています。 よってこれは自然数であると言えます。また別の例として、 を空集合「
を空集合「 」で表し、数
」で表し、数 に対して次の数を「
に対して次の数を「



 」で表すと、「
」で表すと、「

 」「
」「













 」「
」「























 」「(中略)
」「(中略)








 」「
」「









 」となっていきます。 これもペアノの公理を満たすため、これも自然数であると言えます。
」となっていきます。 これもペアノの公理を満たすため、これも自然数であると言えます。
 を空集合「
を空集合「 」で表し、数
」で表し、数 に対して次の数を「
に対して次の数を「



 」で表すと、「
」で表すと、「

 」「
」「













 」「
」「























 」「(中略)
」「(中略)








 」「
」「









 」となっていきます。 これもペアノの公理を満たすため、これも自然数であると言えます。
」となっていきます。 これもペアノの公理を満たすため、これも自然数であると言えます。このように、いくつもの方法で集合から自然数が構築できます。 具体的にどの方法で自然数を構築したかは重要ではなく、ペアノの公理を満たしていればどの方法でも構いません。 以後、このように構築された自然数を改めて「













 」という集合で表すことにします。
」という集合で表すことにします。














 」という集合で表すことにします。
」という集合で表すことにします。3.公理的集合論
3.1ラッセルのパラドックス
と、ここまである程度直感的に話を進めてきましたが、このように直感的に集合を扱うと、論理的に破綻することが判っています。 その一つの例が、「ラッセルのパラドックス」です。 ラッセルのパラドックスとは以下の通りです。
まず、単語であるものをすべて集めた集合「単語」を考えてみます。 このとき「単語」自身も単語なので、この集合に属します。 つまり、「単語
 イヌ
イヌ リンゴ
リンゴ 単語
単語

 」のようになります。
」のようになります。

 イヌ
イヌ リンゴ
リンゴ 単語
単語

 」のようになります。
」のようになります。次に、絵文字であるものをすべて集めた集合「絵文字」を考えます。 このとき「絵文字」自身は絵文字ではないので、この集合には属しません。 つまり、「絵文字








 」のようになります。
」のようになります。









 」のようになります。
」のようになります。このように考えると、集合とは2つのタイプに分けられ、この「単語」のように「自分自身が属する集合」と、この「絵文字」のように「自分自身が属さない集合」が存在することになります。
ここで、「自分自身が属さない集合」をすべて集めた集合を考えてみましょう。 つまり「絵文字」は「自分自身が属さない集合」でしたので、「自分自身が属さない集合
 絵文字
絵文字

 」となります。 さてこのとき、この集合には自分自身が属するでしょうか。 すなわち、「自分自身が属さない集合
」となります。 さてこのとき、この集合には自分自身が属するでしょうか。 すなわち、「自分自身が属さない集合
 絵文字
絵文字 自分自身が属さない集合
自分自身が属さない集合

 」となるでしょうか。
」となるでしょうか。

 絵文字
絵文字

 」となります。 さてこのとき、この集合には自分自身が属するでしょうか。 すなわち、「自分自身が属さない集合
」となります。 さてこのとき、この集合には自分自身が属するでしょうか。 すなわち、「自分自身が属さない集合
 絵文字
絵文字 自分自身が属さない集合
自分自身が属さない集合

 」となるでしょうか。
」となるでしょうか。仮に自分自身が属するとした場合、「自分自身が属さない集合」なのに属しているので矛盾しています。 また仮に自分自身が属さないとした場合、「自分自身が属さない集合」という条件を満たしているので、この集合に属するべきとなって矛盾することになります。
第1話で説明した通り、命題は真か偽かのいずれかである必要があるため、このような問いは命題になりえません。 つまり「自分自身が属さない集合をすべて集めた集合」のような集合を認めてしまうと、論理的破綻を招くのです。
3.2公理的集合論
そこで、集合を「ものの集まり」のような直感的な定義ではなく、何が集合であるかを厳密に定めた「公理」によって集合を定義する流れが生まれました。 これは「公理的集合論(こうりてきしゅうごうろん)」と呼ばれます。 直感的なほうは「素朴集合論(そぼくしゅうごうろん)」と呼ばれます。
4.加算の公理
それでは、いよいよ最後に「



 」を証明してみましょう。 ここまでで定義した自然数に対して、以下の公理を追加します。
」を証明してみましょう。 ここまでで定義した自然数に対して、以下の公理を追加します。




 」を証明してみましょう。 ここまでで定義した自然数に対して、以下の公理を追加します。
」を証明してみましょう。 ここまでで定義した自然数に対して、以下の公理を追加します。

 が自然数であるとき、
が自然数であるとき、
ただし自然数 に対し「
に対し「
 」とは、「
」とは、「 の次の数」を表す。
の次の数」を表す。
これを、「加算(かさん)の公理(こうり)」といいます。 この公理を使うと「



 」が証明できます。 以下の通りです。
」が証明できます。 以下の通りです。




 」が証明できます。 以下の通りです。
」が証明できます。 以下の通りです。- 以下、「


 」を変形して「
」を変形して「 」にしていく。
」にしていく。 - 自然数の定義より、







 。(「0′」、すなわち0の次の数は、自然数の定義で1と定義していました。)
。(「0′」、すなわち0の次の数は、自然数の定義で1と定義していました。) - 加算の公理2より










 なので、
なので、









 。
。 - 加算の公理1より




 なので、
なので、









 。
。  の次の数は
の次の数は なので、
なので、




 。
。- よって、




 。(証明終)
。(証明終)
加算の公理を機械的に適用していくだけで、「

 」から「
」から「 」が導出できています。 同様に「
」が導出できています。 同様に「



 」「
」「









 」なども証明できますので試してみてください。
」なども証明できますので試してみてください。


 」から「
」から「 」が導出できています。 同様に「
」が導出できています。 同様に「



 」「
」「









 」なども証明できますので試してみてください。
」なども証明できますので試してみてください。今回は、集合を使って自然数を定義し、加算の公理を用いて「



 」を証明しました。 次回は、自然数に負の数を含めた「整数」をはじめとするさまざまな数をお話します!
」を証明しました。 次回は、自然数に負の数を含めた「整数」をはじめとするさまざまな数をお話します!




 」を証明しました。 次回は、自然数に負の数を含めた「整数」をはじめとするさまざまな数をお話します!
」を証明しました。 次回は、自然数に負の数を含めた「整数」をはじめとするさまざまな数をお話します!

