1順列
1.1順列の例題
 個の異なるものから、
個の異なるものから、 個を抜き出して並べるパターンの数を、「順列」といい「
個を抜き出して並べるパターンの数を、「順列」といい「
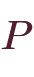
 」と表します。
」と表します。例題を見てみましょう(図1-1)。
「 」から「
」から「 」が書かれた
」が書かれた 枚のカードから、
枚のカードから、 枚を引いて並べて
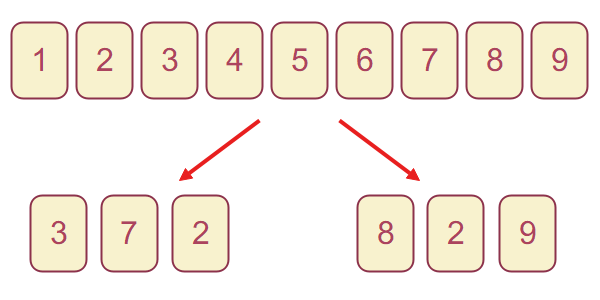
枚を引いて並べて 桁の数を作るとする。 作れる数は何通りか。
桁の数を作るとする。 作れる数は何通りか。
図1-2のイメージです。
何パターンあるのか、解いてみましょう。
 桁の数に使ったカードを、左から順に1枚目、2枚目、3枚目としたとき、まず1枚目になる候補は
桁の数に使ったカードを、左から順に1枚目、2枚目、3枚目としたとき、まず1枚目になる候補は 通りあります。 次に2枚目になる候補は、1枚減っているので
通りあります。 次に2枚目になる候補は、1枚減っているので 通りです。 そして3枚目になる候補は、さらに1枚減っているので
通りです。 そして3枚目になる候補は、さらに1枚減っているので 通りです。 よってパターンの数は、「
通りです。 よってパターンの数は、「







 通り」が答えです。
通り」が答えです。1.2順列の公式
一般に、 個の異なるものから
個の異なるものから 個を抜き出して並べるパターンの数
個を抜き出して並べるパターンの数
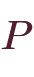
 は、「
は、「
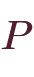
























 」で求まります。
」で求まります。
 個の異なるものから
個の異なるものから 個を抜き出して並べるパターンの数
個を抜き出して並べるパターンの数
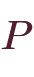
 は、「
は、「
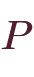
























 」で求まります。
」で求まります。また「
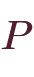
 」は、「
」は、「













 」から「
」から「























 」を除いたものなので、階乗「
」を除いたものなので、階乗「










 」を使うと「
」を使うと「
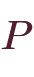














 」と表せます。
」と表せます。

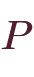
 」は、「
」は、「













 」から「
」から「























 」を除いたものなので、階乗「
」を除いたものなので、階乗「










 」を使うと「
」を使うと「
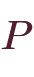














 」と表せます。
」と表せます。ちなみに、 個の異なるものを全部並べ替えるパターンの数は、「
個の異なるものを全部並べ替えるパターンの数は、「 個のものから
個のものから 個を抜き出して並べるパターン」とも考えられるため、「
個を抜き出して並べるパターン」とも考えられるため、「
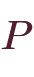

















 」で求まります。
」で求まります。
 個の異なるものを全部並べ替えるパターンの数は、「
個の異なるものを全部並べ替えるパターンの数は、「 個のものから
個のものから 個を抜き出して並べるパターン」とも考えられるため、「
個を抜き出して並べるパターン」とも考えられるため、「
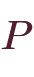

















 」で求まります。
」で求まります。2組合せ
2.1組合せの例題
 個の異なるものから、
個の異なるものから、 個を抜き出す組み合わせのパターンの数を、「組合せ」といい「
個を抜き出す組み合わせのパターンの数を、「組合せ」といい「

 」と表します。
」と表します。例題を見てみましょう(図2-1)。
「 」から「
」から「 」が書かれた
」が書かれた 枚のカードから、同時に
枚のカードから、同時に 枚を引くときの組み合わせは何通りか。
枚を引くときの組み合わせは何通りか。
順列のときとは違い、「



 」と「
」と「



 」を区別しません。 解いてみましょう。
」を区別しません。 解いてみましょう。




 」と「
」と「



 」を区別しません。 解いてみましょう。
」を区別しません。 解いてみましょう。まず 枚のカードから
枚のカードから 枚を引く順列を求めます。
枚を引く順列を求めます。 
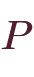
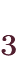









 通りです。
通りです。
 枚のカードから
枚のカードから 枚を引く順列を求めます。
枚を引く順列を求めます。 
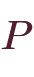
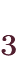









 通りです。
通りです。しかしこの

 通りの中には、順番が違うだけの重複があります。 例えば「
通りの中には、順番が違うだけの重複があります。 例えば「



 」「
」「



 」「
」「



 」「
」「



 」「
」「



 」「
」「



 」です。 これは、引いた
」です。 これは、引いた 枚には、その
枚には、その 枚を並べ替えるパターンである「
枚を並べ替えるパターンである「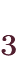
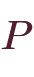
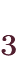




 」通りが余分に数えられているため、本来よりも
」通りが余分に数えられているため、本来よりも 倍多く数えられていることになります。
倍多く数えられていることになります。


 通りの中には、順番が違うだけの重複があります。 例えば「
通りの中には、順番が違うだけの重複があります。 例えば「



 」「
」「



 」「
」「



 」「
」「



 」「
」「



 」「
」「



 」です。 これは、引いた
」です。 これは、引いた 枚には、その
枚には、その 枚を並べ替えるパターンである「
枚を並べ替えるパターンである「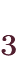
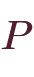
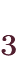




 」通りが余分に数えられているため、本来よりも
」通りが余分に数えられているため、本来よりも 倍多く数えられていることになります。
倍多く数えられていることになります。そこで、

 通りを
通りを で割って、「
で割って、「






 通り」が答えです。
通り」が答えです。


 通りを
通りを で割って、「
で割って、「






 通り」が答えです。
通り」が答えです。2.2組合せの公式
一般に、 個の異なるものから
個の異なるものから 個を抜き出す組み合わせのパターンの数
個を抜き出す組み合わせのパターンの数

 は、「
は、「





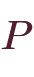






 」で求まります。
」で求まります。
 個の異なるものから
個の異なるものから 個を抜き出す組み合わせのパターンの数
個を抜き出す組み合わせのパターンの数

 は、「
は、「





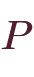






 」で求まります。
」で求まります。また、 枚のカードから
枚のカードから 枚を選ぶことは、選ばれずに残った
枚を選ぶことは、選ばれずに残った 枚のカード側に着目すると、
枚のカード側に着目すると、 枚のカードから
枚のカードから 枚を選んだことと同じになります。 つまり
枚を選んだことと同じになります。 つまり

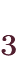



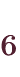 が成り立ちます。 一般に、
が成り立ちます。 一般に、





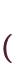


 が成り立ちます。
が成り立ちます。
 枚のカードから
枚のカードから 枚を選ぶことは、選ばれずに残った
枚を選ぶことは、選ばれずに残った 枚のカード側に着目すると、
枚のカード側に着目すると、 枚のカードから
枚のカードから 枚を選んだことと同じになります。 つまり
枚を選んだことと同じになります。 つまり

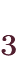



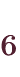 が成り立ちます。 一般に、
が成り立ちます。 一般に、







 が成り立ちます。
が成り立ちます。

 は、図2-2のように、括弧内に縦に並べる記法で書かれることもありますが、意味は
は、図2-2のように、括弧内に縦に並べる記法で書かれることもありますが、意味は

 と同じです。
と同じです。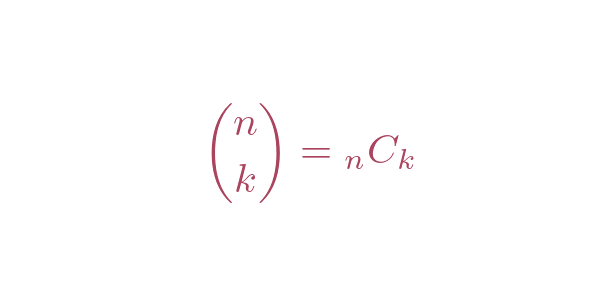
3重複順列
3.1重複順列の例題
 個の異なるものから、何度も同じものが選べるときに
個の異なるものから、何度も同じものが選べるときに 個を選んで並べるパターンの数を、「重複順列」といいます。
個を選んで並べるパターンの数を、「重複順列」といいます。例題を見てみましょう(図3-1)。
「 」から「
」から「 」が書かれた
」が書かれた 種類のカードがそれぞれたくさんある。 ここから
種類のカードがそれぞれたくさんある。 ここから 枚を選んで並べて
枚を選んで並べて 桁の数を作るとする。 作れる数は何通りか。
桁の数を作るとする。 作れる数は何通りか。
解き方は、同じ数字のカードを何回も選べるため、毎回 通りの選び方があることから、「
通りの選び方があることから、「







 」が答えです。
」が答えです。
 通りの選び方があることから、「
通りの選び方があることから、「







 」が答えです。
」が答えです。3.2重複順列の公式
一般に、 個の異なるものから重複を許して、
個の異なるものから重複を許して、 個選んで並べるパターンの数は、「
個選んで並べるパターンの数は、「
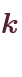 」で求まります。
」で求まります。
 個の異なるものから重複を許して、
個の異なるものから重複を許して、 個選んで並べるパターンの数は、「
個選んで並べるパターンの数は、「
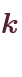 」で求まります。
」で求まります。4重複組合せ
4.1重複組合せの例題
 個の異なるものから、何度も同じものが選べるときに
個の異なるものから、何度も同じものが選べるときに 個を選ぶ組み合わせのパターンの数を、「重複組合せ」といいます。
個を選ぶ組み合わせのパターンの数を、「重複組合せ」といいます。例題を見てみましょう(図4-1)。
「 」から「
」から「 」が書かれた
」が書かれた 種類のカードがそれぞれたくさんある。 ここから同時に
種類のカードがそれぞれたくさんある。 ここから同時に 枚を選ぶとき、カードに書かれた数の組み合わせは何通りか。
枚を選ぶとき、カードに書かれた数の組み合わせは何通りか。
 種類は複雑なので、まずは
種類は複雑なので、まずは 種類のカードで考えてみましょう。
種類のカードで考えてみましょう。「 」「
」「 」の
」の 種類のカードを重複を許して
種類のカードを重複を許して 枚選ぶ組み合わせ方とは、見方を変えると、
枚選ぶ組み合わせ方とは、見方を変えると、 枚のどこで仕切るかという考え方に置き換えられます(図4-2)。
枚のどこで仕切るかという考え方に置き換えられます(図4-2)。
 」「
」「 」の
」の 種類のカードを重複を許して
種類のカードを重複を許して 枚選ぶ組み合わせ方とは、見方を変えると、
枚選ぶ組み合わせ方とは、見方を変えると、 枚のどこで仕切るかという考え方に置き換えられます(図4-2)。
枚のどこで仕切るかという考え方に置き換えられます(図4-2)。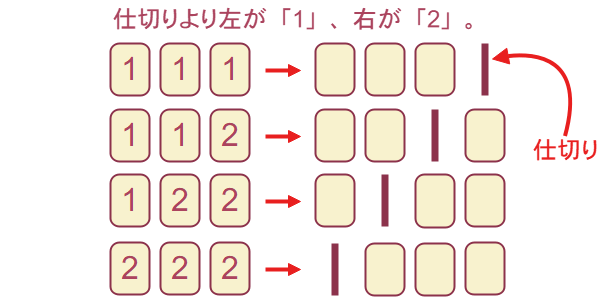
 枚選んだカードのうち、仕切りより左側を「
枚選んだカードのうち、仕切りより左側を「 」とし、右側を「
」とし、右側を「 」としています。
」としています。そしてこれは、「 か所のうち、仕切りをどこに置くか」という問題に置き換えられるため、
か所のうち、仕切りをどこに置くか」という問題に置き換えられるため、 か所から
か所から か所を選ぶ、
か所を選ぶ、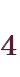



 通りと求められます。
通りと求められます。
 か所のうち、仕切りをどこに置くか」という問題に置き換えられるため、
か所のうち、仕切りをどこに置くか」という問題に置き換えられるため、 か所から
か所から か所を選ぶ、
か所を選ぶ、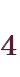



 通りと求められます。
通りと求められます。同様に、カードが「 」から「
」から「 」までの
」までの 種類の場合にも、仕切りの考え方に直せます(図4-3)。
種類の場合にも、仕切りの考え方に直せます(図4-3)。
 」から「
」から「 」までの
」までの 種類の場合にも、仕切りの考え方に直せます(図4-3)。
種類の場合にも、仕切りの考え方に直せます(図4-3)。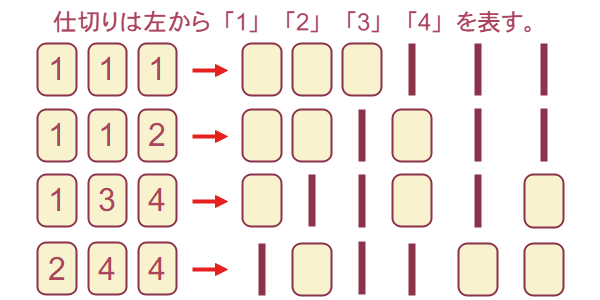
これも同様に、 か所から仕切りをおく
か所から仕切りをおく か所を選ぶ組み合わせとなるため、
か所を選ぶ組み合わせとなるため、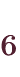

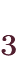


 通りと求められます。
通りと求められます。
 か所から仕切りをおく
か所から仕切りをおく か所を選ぶ組み合わせとなるため、
か所を選ぶ組み合わせとなるため、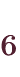

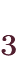


 通りと求められます。
通りと求められます。例題に戻ると、 種類のカードの場合には仕切りが
種類のカードの場合には仕切りが 個となるため、カード
個となるため、カード 枚と仕切りを合わせた
枚と仕切りを合わせた




 か所から
か所から か所を選ぶ組み合わせとなります。 よって、「
か所を選ぶ組み合わせとなります。 よって、「


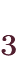



 通り」が答えです。
通り」が答えです。
 種類のカードの場合には仕切りが
種類のカードの場合には仕切りが 個となるため、カード
個となるため、カード 枚と仕切りを合わせた
枚と仕切りを合わせた




 か所から
か所から か所を選ぶ組み合わせとなります。 よって、「
か所を選ぶ組み合わせとなります。 よって、「


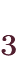



 通り」が答えです。
通り」が答えです。4.2重複組合せの公式
一般に、 個の異なるものから重複を許して、
個の異なるものから重複を許して、 個選ぶ組み合わせのパターンの数は、仕切りの数が
個選ぶ組み合わせのパターンの数は、仕切りの数が

 個となるため、「
個となるため、「


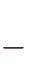


 」で求まります。
」で求まります。
 個の異なるものから重複を許して、
個の異なるものから重複を許して、 個選ぶ組み合わせのパターンの数は、仕切りの数が
個選ぶ組み合わせのパターンの数は、仕切りの数が

 個となるため、「
個となるため、「


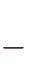


 」で求まります。
」で求まります。