1全単射と逆写像の定理
今回証明する定理は、こちらのページで紹介した、図1-1です。
「写像が全単射であること」と「写像に逆写像が存在すること」は同値である。 また、写像の逆写像は全単射である。
まずは、「写像が全単射であること」と「写像に逆写像が存在すること」が同値であることを証明します。 命題 と
と が同値であることは、「
が同値であることは、「

 」かつ「
」かつ「

 」であることを意味するので、これらを順番に証明します。
」であることを意味するので、これらを順番に証明します。
 と
と が同値であることは、「
が同値であることは、「

 」かつ「
」かつ「

 」であることを意味するので、これらを順番に証明します。
」であることを意味するので、これらを順番に証明します。1.1全単射ならば逆写像が存在する
まず、「写像が全単射である」ならば「写像に逆写像が存在する」ことを証明しましょう。
写像



 が全単射であるとします。 このとき、
が全単射であるとします。 このとき、 は全射なので、任意の
は全射なので、任意の

 について
について




 を満たす
を満たす が存在します。 また
が存在します。 また は単射なので、このような
は単射なので、このような は複数存在せず、
は複数存在せず、 ごとに1つだけ存在します。
ごとに1つだけ存在します。




 が全単射であるとします。 このとき、
が全単射であるとします。 このとき、 は全射なので、任意の
は全射なので、任意の

 について
について




 を満たす
を満たす が存在します。 また
が存在します。 また は単射なので、このような
は単射なので、このような は複数存在せず、
は複数存在せず、 ごとに1つだけ存在します。
ごとに1つだけ存在します。ここで写像



 を考え、任意の
を考え、任意の

 に対して1つだけ存在する、
に対して1つだけ存在する、




 を満たす
を満たす を対応付ける写像
を対応付ける写像




 だとします。 このとき、任意の
だとします。 このとき、任意の





 に対し、
に対し、




 ならば
ならば




 であり、
であり、




 ならば
ならば




 であると言えますので、
であると言えますので、 は
は の逆写像となります。
の逆写像となります。




 を考え、任意の
を考え、任意の

 に対して1つだけ存在する、
に対して1つだけ存在する、




 を満たす
を満たす を対応付ける写像
を対応付ける写像




 だとします。 このとき、任意の
だとします。 このとき、任意の





 に対し、
に対し、




 ならば
ならば




 であり、
であり、




 ならば
ならば




 であると言えますので、
であると言えますので、 は
は の逆写像となります。
の逆写像となります。よって、写像が全単射ならば、写像に逆写像が存在すると言えました。
1.2逆写像ならば全単射が存在する
次に、「写像に逆写像が存在する」ならば「写像が全単射である」ことを証明しましょう。
写像



 に逆写像
に逆写像





 が存在するとします。
が存在するとします。




 に逆写像
に逆写像





 が存在するとします。
が存在するとします。このとき、 が全射でないと仮定すると、写像の対応付けがない元
が全射でないと仮定すると、写像の対応付けがない元

 が存在して、任意の元
が存在して、任意の元

 に対し「
に対し「



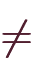
 」となります。 しかし、このような
」となります。 しかし、このような について、逆写像のほうには
について、逆写像のほうには






 となる
となる

 が存在し、
が存在し、




 となるはずですが、任意の元
となるはずですが、任意の元

 に対し「
に対し「



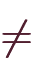
 」となることと矛盾します。 よって、
」となることと矛盾します。 よって、 は全射でなければなりません。
は全射でなければなりません。
 が全射でないと仮定すると、写像の対応付けがない元
が全射でないと仮定すると、写像の対応付けがない元

 が存在して、任意の元
が存在して、任意の元

 に対し「
に対し「



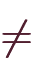
 」となります。 しかし、このような
」となります。 しかし、このような について、逆写像のほうには
について、逆写像のほうには






 となる
となる

 が存在し、
が存在し、




 となるはずですが、任意の元
となるはずですが、任意の元

 に対し「
に対し「



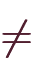
 」となることと矛盾します。 よって、
」となることと矛盾します。 よって、 は全射でなければなりません。
は全射でなければなりません。また、 が単射でないと仮定すると、異なる2つの元「
が単射でないと仮定すると、異なる2つの元「





 (
(

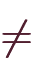

 )」に対し、対応付けの先が重複して
)」に対し、対応付けの先が重複して









 を満たすものがあることになります。 しかし、このとき逆写像のほうには、
を満たすものがあることになります。 しかし、このとき逆写像のほうには、







 と
と







 を満たす
を満たす

 が存在することになりますが、
が存在することになりますが、 を異なる2つの元に対応付けることはできないため、写像の定義に矛盾します。 よって、
を異なる2つの元に対応付けることはできないため、写像の定義に矛盾します。 よって、 は単射でなければなりません。
は単射でなければなりません。
 が単射でないと仮定すると、異なる2つの元「
が単射でないと仮定すると、異なる2つの元「





 (
(

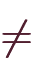

 )」に対し、対応付けの先が重複して
)」に対し、対応付けの先が重複して









 を満たすものがあることになります。 しかし、このとき逆写像のほうには、
を満たすものがあることになります。 しかし、このとき逆写像のほうには、







 と
と







 を満たす
を満たす

 が存在することになりますが、
が存在することになりますが、 を異なる2つの元に対応付けることはできないため、写像の定義に矛盾します。 よって、
を異なる2つの元に対応付けることはできないため、写像の定義に矛盾します。 よって、 は単射でなければなりません。
は単射でなければなりません。よって、 は全射かつ単射なので、写像に逆写像が存在するならば、写像が全単射であると言えました。
は全射かつ単射なので、写像に逆写像が存在するならば、写像が全単射であると言えました。
 は全射かつ単射なので、写像に逆写像が存在するならば、写像が全単射であると言えました。
は全射かつ単射なので、写像に逆写像が存在するならば、写像が全単射であると言えました。以上、「写像が全単射ならば、写像に逆写像が存在する」と「写像に逆写像が存在するならば、写像が全単射である」ことが言えたため、「写像が全単射であること」と「写像に逆写像が存在すること」は同値です。
1.3写像の逆写像は全単射である
最後に、写像の逆写像は全単射であることを証明しましょう。
写像



 に逆写像
に逆写像





 が存在するとします。
が存在するとします。




 に逆写像
に逆写像





 が存在するとします。
が存在するとします。このとき、逆写像の性質より、任意の元

 に対して「
に対して「









 」が成り立ちますので、
」が成り立ちますので、

 の像は、
の像は、



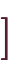

 となり、全射の定義を満たします。 よって、
となり、全射の定義を満たします。 よって、

 は全射です。
は全射です。


 に対して「
に対して「









 」が成り立ちますので、
」が成り立ちますので、

 の像は、
の像は、


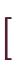

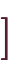

 となり、全射の定義を満たします。 よって、
となり、全射の定義を満たします。 よって、

 は全射です。
は全射です。また、ある元





 に対し、「
に対し、「













 」であるにもかかわらず、「
」であるにもかかわらず、「

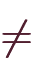

 」となるものがあると仮定します。 すると、
」となるものがあると仮定します。 すると、













 より、「
より、「



















 」となりますが、これは「左辺
」となりますが、これは「左辺












 」「右辺
」「右辺












 」より、「
」より、「



 」となるため矛盾します。 よって、
」となるため矛盾します。 よって、













 のときには、必ず
のときには、必ず



 でなければならないため、
でなければならないため、

 は単射の定義を満たします。 よって、
は単射の定義を満たします。 よって、

 は単射です。
は単射です。






 に対し、「
に対し、「













 」であるにもかかわらず、「
」であるにもかかわらず、「

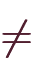

 」となるものがあると仮定します。 すると、
」となるものがあると仮定します。 すると、













 より、「
より、「



















 」となりますが、これは「左辺
」となりますが、これは「左辺












 」「右辺
」「右辺












 」より、「
」より、「



 」となるため矛盾します。 よって、
」となるため矛盾します。 よって、













 のときには、必ず
のときには、必ず



 でなければならないため、
でなければならないため、

 は単射の定義を満たします。 よって、
は単射の定義を満たします。 よって、

 は単射です。
は単射です。以上、

 は全射かつ単射であるため、
は全射かつ単射であるため、

 は全単射です。 よって、写像の逆写像は全単射になります。 (証明終)
は全単射です。 よって、写像の逆写像は全単射になります。 (証明終)


 は全射かつ単射であるため、
は全射かつ単射であるため、

 は全単射です。 よって、写像の逆写像は全単射になります。 (証明終)
は全単射です。 よって、写像の逆写像は全単射になります。 (証明終)