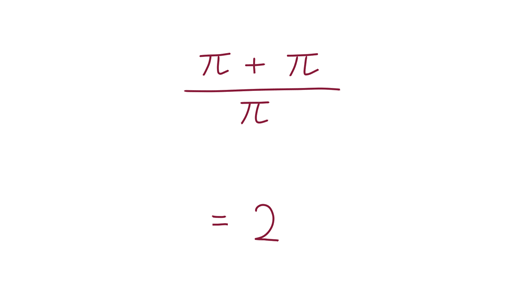2025年09月13日くいなちゃん
 と四則演算と累乗を使って、円周率
と四則演算と累乗を使って、円周率 を作ってみましょう。
を作ってみましょう。
問題
 と四則演算と累乗を組み合わせて、円周率
と四則演算と累乗を組み合わせて、円周率 を作りなさい。 ただし、
を作りなさい。 ただし、







 まで一致していれば良いものとする。
まで一致していれば良いものとする。
今回は、この問題に挑戦してみましょう。
1ライプニッツの公式
さて、図1-1のように計算し続けていくと、限りなく の値に近づいていきますが、
の値に近づいていきますが、







 まで一致する頃にはとても長い計算式になってしまいます。
まで一致する頃にはとても長い計算式になってしまいます。
 の値に近づいていきますが、
の値に近づいていきますが、







 まで一致する頃にはとても長い計算式になってしまいます。
まで一致する頃にはとても長い計算式になってしまいます。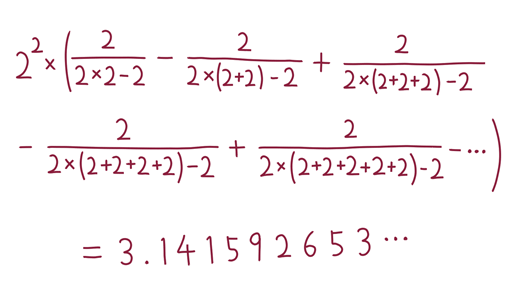
そこで今回はせっかくですので、 の個数がなるべく少なくなる答えを求めてみましょう。
の個数がなるべく少なくなる答えを求めてみましょう。
 の個数がなるべく少なくなる答えを求めてみましょう。
の個数がなるべく少なくなる答えを求めてみましょう。22進数
まず安直に浮かぶのは、2進数で表す方法です。 目標は







 という有限精度の小数なので、これを2進数の小数に変換して、
という有限精度の小数なので、これを2進数の小数に変換して、
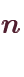 の和で表せば、一つの答えになるはずです。
の和で表せば、一つの答えになるはずです。








 という有限精度の小数なので、これを2進数の小数に変換して、
という有限精度の小数なので、これを2進数の小数に変換して、
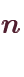 の和で表せば、一つの答えになるはずです。
の和で表せば、一つの答えになるはずです。







 に一致する最短桁数の2進数を計算すると「11.00100100001111110110101」になりましたので、これを
に一致する最短桁数の2進数を計算すると「11.00100100001111110110101」になりましたので、これを
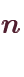 の和に変換すると、図2-1のようになります。
の和に変換すると、図2-1のようになります。
これでもまだ累乗の部分に 以外の数が使われていますので、これらも
以外の数が使われていますので、これらも で表そうとすると相当な長さになりそうです。 諦めて別の方法を探しましょう。
で表そうとすると相当な長さになりそうです。 諦めて別の方法を探しましょう。
 以外の数が使われていますので、これらも
以外の数が使われていますので、これらも で表そうとすると相当な長さになりそうです。 諦めて別の方法を探しましょう。
で表そうとすると相当な長さになりそうです。 諦めて別の方法を探しましょう。3カステヤノスさんの公式
円周率の近似値を求める公式が既にいくつも発見されていますので、それをアレンジすることを考えてみます。








 に一致するシンプルな数式として、ダリオ・カステヤノスさんという方が発見した公式を変形して使ってみます(図3-1)。
に一致するシンプルな数式として、ダリオ・カステヤノスさんという方が発見した公式を変形して使ってみます(図3-1)。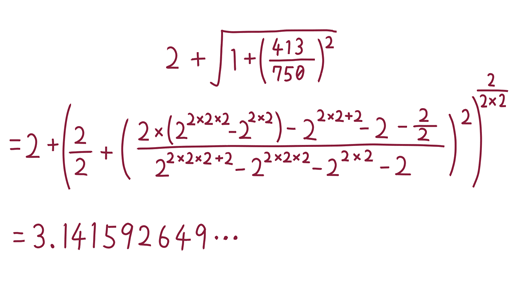
この式により、円周率 は合計35個の
は合計35個の によって表すことができました。 元がシンプルな式でも、
によって表すことができました。 元がシンプルな式でも、 だけで表すと意外と複雑になることが解ります。
だけで表すと意外と複雑になることが解ります。
 は合計35個の
は合計35個の によって表すことができました。 元がシンプルな式でも、
によって表すことができました。 元がシンプルな式でも、 だけで表すと意外と複雑になることが解ります。
だけで表すと意外と複雑になることが解ります。4ラマヌジャンの公式
さて、インドの魔術師と呼ばれた数学者、ラマヌジャンの公式を用いれば、さらに少ない個数の で円周率
で円周率 が表せることに気付きました(図4-1)。
が表せることに気付きました(図4-1)。
 で円周率
で円周率 が表せることに気付きました(図4-1)。
が表せることに気付きました(図4-1)。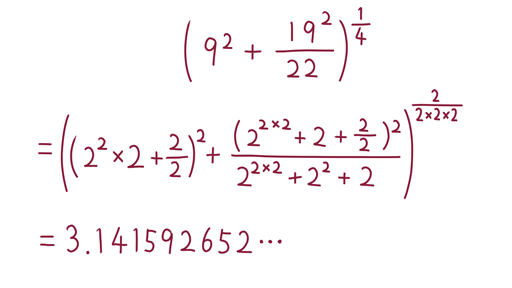
 の個数は、たったの23個となっています。
の個数は、たったの23個となっています。5くいなちゃんの公式
さらに少ない個数の で、円周率
で、円周率 を表せないでしょうか。 他の公式を使っても、これ以上はなかなかシンプルに表せませんでした。
を表せないでしょうか。 他の公式を使っても、これ以上はなかなかシンプルに表せませんでした。
 で、円周率
で、円周率 を表せないでしょうか。 他の公式を使っても、これ以上はなかなかシンプルに表せませんでした。
を表せないでしょうか。 他の公式を使っても、これ以上はなかなかシンプルに表せませんでした。そこで、自力で生み出すことを考えました。 わたしが気合いで試行錯誤した結果、図5-1のような式を生み出すことができました。
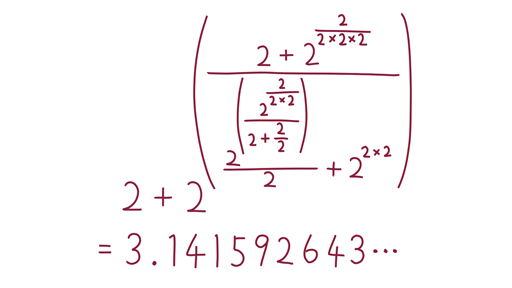
「くいなちゃんの公式」とでも名付けましょう。 これにより、合計20個の で円周率
で円周率 を表すことができました。
を表すことができました。
 で円周率
で円周率 を表すことができました。
を表すことができました。ひょっとしたら更に少ない で、円周率
で、円周率 を表すことも可能かもしれません。 みなさんも是非、挑戦してみてください!
を表すことも可能かもしれません。 みなさんも是非、挑戦してみてください!
 で、円周率
で、円周率 を表すことも可能かもしれません。 みなさんも是非、挑戦してみてください!
を表すことも可能かもしれません。 みなさんも是非、挑戦してみてください!6πで2を作る
最後に、逆に「 で
で を作ることはできないか」と思い至ったのですが、考えるまでもありませんでした(図6-1)。
を作ることはできないか」と思い至ったのですが、考えるまでもありませんでした(図6-1)。
 で
で を作ることはできないか」と思い至ったのですが、考えるまでもありませんでした(図6-1)。
を作ることはできないか」と思い至ったのですが、考えるまでもありませんでした(図6-1)。