1確率と積分
「確率」というものは、ここで改めて説明するまでもなく日常的に使われていて、例えばコインの表が出る確率は

 とか、サイコロの
とか、サイコロの が出る確率は
が出る確率は

 などと理解していることだと思います。
などと理解していることだと思います。


 とか、サイコロの
とか、サイコロの が出る確率は
が出る確率は

 などと理解していることだと思います。
などと理解していることだと思います。しかし特に無限大が絡んでくると、直感的な定義では本当に正しい確率が求まっているのかが判らなくなることがあります。 そこで現代の数学では、第8回で説明した「測度」や「ルベーグ積分」を使って確率を定義することで、直感から離れて厳密に計算できるようになっています。
1.1素朴な確率の定義
まずは測度を使わない、素朴な確率の定義を見ていきましょう。
まず、発生しうる結果を「標本」といい、標本全体の集合を「標本空間」といいます。 例えばサイコロを振る場合、標本は「









 」です。 また標本空間を
」です。 また標本空間を で表すと、
で表すと、













 となります。
となります。










 」です。 また標本空間を
」です。 また標本空間を で表すと、
で表すと、













 となります。
となります。このうち例えば、「サイコロを振って目が か
か か
か の場合」を考えると、これは標本空間の部分集合になります。 このような標本空間の部分集合のことを「事象」といいます。 この例では事象を
の場合」を考えると、これは標本空間の部分集合になります。 このような標本空間の部分集合のことを「事象」といいます。 この例では事象を とすると
とすると







 と書けます。
と書けます。
 か
か か
か の場合」を考えると、これは標本空間の部分集合になります。 このような標本空間の部分集合のことを「事象」といいます。 この例では事象を
の場合」を考えると、これは標本空間の部分集合になります。 このような標本空間の部分集合のことを「事象」といいます。 この例では事象を とすると
とすると







 と書けます。
と書けます。以上を元に、確率を図1-1のように定義します。
どの標本が発生することも同程度に確からしいとき、事象

 が発生する確率
が発生する確率


 は、
は、










 である。 ただし、
である。 ただし、





 とは、それぞれ
とは、それぞれ

 の元の数とする。
の元の数とする。
例えばサイコロを振って偶数が出る確率は、「









 」のどの標本が発生することも同程度に確からしいとすると、
」のどの標本が発生することも同程度に確からしいとすると、



















 、
、













 より、
より、
















 です。
です。










 」のどの標本が発生することも同程度に確からしいとすると、
」のどの標本が発生することも同程度に確からしいとすると、



















 、
、













 より、
より、
















 です。
です。しかしこの定義では、例えばサイコロを何回振るか判らないときに、無限回を考慮する必要が出て

 が無限大になって計算できなかったり、また「どの標本が発生することも同程度に確からしいとき」以外の確率が計算できないという問題があります。
が無限大になって計算できなかったり、また「どの標本が発生することも同程度に確からしいとき」以外の確率が計算できないという問題があります。


 が無限大になって計算できなかったり、また「どの標本が発生することも同程度に確からしいとき」以外の確率が計算できないという問題があります。
が無限大になって計算できなかったり、また「どの標本が発生することも同程度に確からしいとき」以外の確率が計算できないという問題があります。1.2測度論による確率の定義
そこで、測度を使ってここまでの定義を一般化します。 結局確率とは、 から
から の区間のうちどれだけを占めるかという「長さ」の問題になりますので、測度や積分の話に還元できることになります。
の区間のうちどれだけを占めるかという「長さ」の問題になりますので、測度や積分の話に還元できることになります。
 から
から の区間のうちどれだけを占めるかという「長さ」の問題になりますので、測度や積分の話に還元できることになります。
の区間のうちどれだけを占めるかという「長さ」の問題になりますので、測度や積分の話に還元できることになります。測度を使った確率の定義は図1-2の通りです。
測度空間





 において、
において、




 であるとき、
であるとき、





 を確率空間と呼び、
を確率空間と呼び、 を確率と呼ぶ。
を確率と呼ぶ。
よく解らないと思いますので、第8回で説明した測度をおさらいしつつ補足します。 サイコロを振って偶数が出る確率を求めてみましょう。
まず測度空間





 とは、任意の集合「
とは、任意の集合「 」と、測れる仕組みを整えた
」と、測れる仕組みを整えた -加法族「
-加法族「 」と、それらに対して測り方を定めた測度「
」と、それらに対して測り方を定めた測度「 」を一組にしたものでした。
」を一組にしたものでした。






 とは、任意の集合「
とは、任意の集合「 」と、測れる仕組みを整えた
」と、測れる仕組みを整えた -加法族「
-加法族「 」と、それらに対して測り方を定めた測度「
」と、それらに対して測り方を定めた測度「 」を一組にしたものでした。
」を一組にしたものでした。ここで集合 は、標本空間としておきます。 サイコロの場合、
は、標本空間としておきます。 サイコロの場合、













 です。
です。
 は、標本空間としておきます。 サイコロの場合、
は、標本空間としておきます。 サイコロの場合、













 です。
です。 -加法族
-加法族 は多くの場合、
は多くの場合、 のすべての事象を集めた集合とします。 つまりサイコロの場合、
のすべての事象を集めた集合とします。 つまりサイコロの場合、













































 のように全パターンを列挙したものになります。
のように全パターンを列挙したものになります。測度 は、
は、 -加法族の任意の部分集合に対し、長さを返す関数です。
-加法族の任意の部分集合に対し、長さを返す関数です。 






 などとすると何らかの長さを返すイメージです。
などとすると何らかの長さを返すイメージです。
 は、
は、 -加法族の任意の部分集合に対し、長さを返す関数です。
-加法族の任意の部分集合に対し、長さを返す関数です。 






 などとすると何らかの長さを返すイメージです。
などとすると何らかの長さを返すイメージです。また先ほどの定義に「




 であるとき
であるとき を確率と呼ぶ」とありますが、これは確率として当然のことで、各標本の確率を全部合わせると
を確率と呼ぶ」とありますが、これは確率として当然のことで、各標本の確率を全部合わせると であることを意味しています。 例えば、素朴な確率の定義で示した「
であることを意味しています。 例えば、素朴な確率の定義で示した「










 」を測度だとみなすと、
」を測度だとみなすと、












 となりますので一つの確率だといえます。
となりますので一つの確率だといえます。





 であるとき
であるとき を確率と呼ぶ」とありますが、これは確率として当然のことで、各標本の確率を全部合わせると
を確率と呼ぶ」とありますが、これは確率として当然のことで、各標本の確率を全部合わせると であることを意味しています。 例えば、素朴な確率の定義で示した「
であることを意味しています。 例えば、素朴な確率の定義で示した「










 」を測度だとみなすと、
」を測度だとみなすと、












 となりますので一つの確率だといえます。
となりますので一つの確率だといえます。測度空間





 があれば、実際に確率が求まります。 例えばサイコロを振って偶数が出る確率を求めたい場合、
があれば、実際に確率が求まります。 例えばサイコロを振って偶数が出る確率を求めたい場合、 -加法族
-加法族 の部分集合
の部分集合





 に対し、
に対し、








 を計算すれば求まるという流れです。
を計算すれば求まるという流れです。 


 の定義を工夫すると、「どの標本が発生することも同程度に確からしい」とはいえない場合の確率も定義できます。 例えば、
の定義を工夫すると、「どの標本が発生することも同程度に確からしい」とはいえない場合の確率も定義できます。 例えば、 に
に が属しているときには
が属しているときには




 、属していないときには
、属していないときには




 と定義することで、「必ず
と定義することで、「必ず が出るサイコロの確率」といったものも定義できます。
が出るサイコロの確率」といったものも定義できます。






 があれば、実際に確率が求まります。 例えばサイコロを振って偶数が出る確率を求めたい場合、
があれば、実際に確率が求まります。 例えばサイコロを振って偶数が出る確率を求めたい場合、 -加法族
-加法族 の部分集合
の部分集合





 に対し、
に対し、








 を計算すれば求まるという流れです。
を計算すれば求まるという流れです。 


 の定義を工夫すると、「どの標本が発生することも同程度に確からしい」とはいえない場合の確率も定義できます。 例えば、
の定義を工夫すると、「どの標本が発生することも同程度に確からしい」とはいえない場合の確率も定義できます。 例えば、 に
に が属しているときには
が属しているときには




 、属していないときには
、属していないときには




 と定義することで、「必ず
と定義することで、「必ず が出るサイコロの確率」といったものも定義できます。
が出るサイコロの確率」といったものも定義できます。2確率の主な性質
さて、確率の主な性質について説明します。
2.1積の法則
まずサイコロを 回振って、「
回振って、「 回目に
回目に が出る場合」と「
が出る場合」と「 回目に偶数が出る場合」の確率を考えましょう。
回目に偶数が出る場合」の確率を考えましょう。
 回振って、「
回振って、「 回目に
回目に が出る場合」と「
が出る場合」と「 回目に偶数が出る場合」の確率を考えましょう。
回目に偶数が出る場合」の確率を考えましょう。「 回目に
回目に が出る事象」を
が出る事象」を とし、「
とし、「 回目に偶数が出る事象」を
回目に偶数が出る事象」を とします。 すると、それぞれの確率は
とします。 すると、それぞれの確率は



















 と求まります。
と求まります。
 回目に
回目に が出る事象」を
が出る事象」を とし、「
とし、「 回目に偶数が出る事象」を
回目に偶数が出る事象」を とします。 すると、それぞれの確率は
とします。 すると、それぞれの確率は



















 と求まります。
と求まります。このとき、「 回目に
回目に が出て、かつ
が出て、かつ 回目に偶数が出る確率」は、
回目に偶数が出る確率」は、 回目に出た目が
回目に出た目が 回目に出る目の確率に影響しないため、図2-1のように
回目に出る目の確率に影響しないため、図2-1のように と
と が重なった部分の面積で求まります。
が重なった部分の面積で求まります。
 回目に
回目に が出て、かつ
が出て、かつ 回目に偶数が出る確率」は、
回目に偶数が出る確率」は、 回目に出た目が
回目に出た目が 回目に出る目の確率に影響しないため、図2-1のように
回目に出る目の確率に影響しないため、図2-1のように と
と が重なった部分の面積で求まります。
が重なった部分の面積で求まります。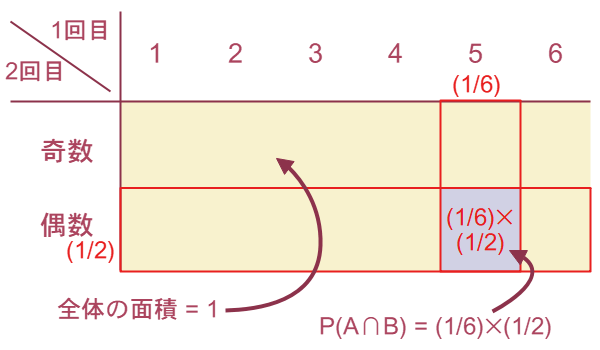
この例のように、事象 と事象
と事象 が互いの確率に影響を与えない場合、
が互いの確率に影響を与えない場合、 と
と は互いに「独立」であるといいます。 一般に、独立な事象
は互いに「独立」であるといいます。 一般に、独立な事象

 に対し、
に対し、 と
と が両方とも起こる確率
が両方とも起こる確率




 とは、「
とは、「














 」のように確率の掛け算で求まります。
」のように確率の掛け算で求まります。
 と事象
と事象 が互いの確率に影響を与えない場合、
が互いの確率に影響を与えない場合、 と
と は互いに「独立」であるといいます。 一般に、独立な事象
は互いに「独立」であるといいます。 一般に、独立な事象

 に対し、
に対し、 と
と が両方とも起こる確率
が両方とも起こる確率




 とは、「
とは、「














 」のように確率の掛け算で求まります。
」のように確率の掛け算で求まります。2.2条件付き確率
次に、 回目に
回目に が出たことが確定した上で、
が出たことが確定した上で、 回目に偶数が出る確率の求め方を説明します。
回目に偶数が出る確率の求め方を説明します。
 回目に
回目に が出たことが確定した上で、
が出たことが確定した上で、 回目に偶数が出る確率の求め方を説明します。
回目に偶数が出る確率の求め方を説明します。 回目に
回目に の目が出て
の目が出て 回目に
回目に の目が出ることを「
の目が出ることを「



 」のように表すことにすると、標本空間はすべてのパターンを網羅して
」のように表すことにすると、標本空間はすべてのパターンを網羅して









































 と表せます。
と表せます。ここで、「既に が起こったとして
が起こったとして が起こる事象」を「
が起こる事象」を「

 」と表すことにします。 すると、そのときの確率
」と表すことにします。 すると、そのときの確率




 、つまり「既に
、つまり「既に 回目に
回目に が出たとして
が出たとして 回目に偶数が出る確率」は図2-2のように求まります。
回目に偶数が出る確率」は図2-2のように求まります。
 が起こったとして
が起こったとして が起こる事象」を「
が起こる事象」を「

 」と表すことにします。 すると、そのときの確率
」と表すことにします。 すると、そのときの確率




 、つまり「既に
、つまり「既に 回目に
回目に が出たとして
が出たとして 回目に偶数が出る確率」は図2-2のように求まります。
回目に偶数が出る確率」は図2-2のように求まります。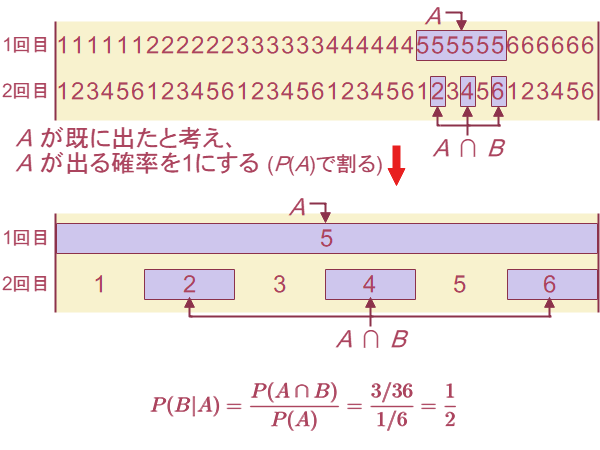
このように、既に が起こったとして
が起こったとして が起こる確率
が起こる確率




 は、「既に
は、「既に が起こった」と考えて
が起こった」と考えて の確率を
の確率を に引き延ばすことにより、
に引き延ばすことにより、
















 で計算できます。
で計算できます。
 が起こったとして
が起こったとして が起こる確率
が起こる確率




 は、「既に
は、「既に が起こった」と考えて
が起こった」と考えて の確率を
の確率を に引き延ばすことにより、
に引き延ばすことにより、
















 で計算できます。
で計算できます。サイコロの例では、 と
と が独立だったため、
が独立だったため、








 と
と






 は一致しましたが、例えば「1組のトランプから2回カードを抜き取って両方ともハートである確率」を考えると、1回目に抜き取ったカードが2回目には無くなっているため、1回目に起こった結果が2回目の確率に影響を与えて、
は一致しましたが、例えば「1組のトランプから2回カードを抜き取って両方ともハートである確率」を考えると、1回目に抜き取ったカードが2回目には無くなっているため、1回目に起こった結果が2回目の確率に影響を与えて、




 と
と


 は一致しません。
は一致しません。
 と
と が独立だったため、
が独立だったため、








 と
と






 は一致しましたが、例えば「1組のトランプから2回カードを抜き取って両方ともハートである確率」を考えると、1回目に抜き取ったカードが2回目には無くなっているため、1回目に起こった結果が2回目の確率に影響を与えて、
は一致しましたが、例えば「1組のトランプから2回カードを抜き取って両方ともハートである確率」を考えると、1回目に抜き取ったカードが2回目には無くなっているため、1回目に起こった結果が2回目の確率に影響を与えて、




 と
と


 は一致しません。
は一致しません。2.3ベイズの定理
さて、




 とは、既に
とは、既に が起こったとして
が起こったとして が起こる確率のことでした。 逆に、既に
が起こる確率のことでした。 逆に、既に が起こったとして
が起こったとして が起こる確率
が起こる確率




 を考えてみましょう。 図2-3の問題です。
を考えてみましょう。 図2-3の問題です。





 とは、既に
とは、既に が起こったとして
が起こったとして が起こる確率のことでした。 逆に、既に
が起こる確率のことでした。 逆に、既に が起こったとして
が起こったとして が起こる確率
が起こる確率




 を考えてみましょう。 図2-3の問題です。
を考えてみましょう。 図2-3の問題です。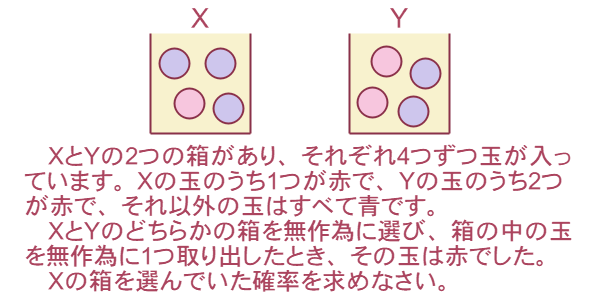
先ほどの
















 の式を変形させていくと、「
の式を変形させていくと、「




















 」という式が導出できます(図2-4)。
」という式が導出できます(図2-4)。

















 の式を変形させていくと、「
の式を変形させていくと、「




















 」という式が導出できます(図2-4)。
」という式が導出できます(図2-4)。(1) 
















 を変形させて、
を変形させて、















 。
。
(2) 
















 を変形させて、
を変形させて、















 。
。
(1)と(2)の式を組み合わせて、



















 より、
より、




















 。
。
この「




















 」の式を「ベイズの定理」といいます。 このベイズの定理を使って、例題を解きましょう。
」の式を「ベイズの定理」といいます。 このベイズの定理を使って、例題を解きましょう。





















 」の式を「ベイズの定理」といいます。 このベイズの定理を使って、例題を解きましょう。
」の式を「ベイズの定理」といいます。 このベイズの定理を使って、例題を解きましょう。 を「Xの箱が選ばれる事象」とし、
を「Xの箱が選ばれる事象」とし、 を「赤い玉が選ばれる事象」とします。 すると、
を「赤い玉が選ばれる事象」とします。 すると、






 はすぐに求まります。
はすぐに求まります。


 は、Xの箱が選ばれて赤い玉が選ばれる確率と、Yの箱が選ばれて赤い玉が選ばれる確率を合わせたものですので、
は、Xの箱が選ばれて赤い玉が選ばれる確率と、Yの箱が選ばれて赤い玉が選ばれる確率を合わせたものですので、














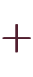













 です。
です。




 は、Xの箱が選ばれて赤い玉が選ばれる確率です。 Xの箱には玉が
は、Xの箱が選ばれて赤い玉が選ばれる確率です。 Xの箱には玉が つあり、そのうち
つあり、そのうち つが赤ですので、単純に
つが赤ですので、単純に








 です。
です。以上をベイズの定理に代入し、「









































 」が答えです。
」が答えです。










































 」が答えです。
」が答えです。2.4加法定理
また、確率の主要な定理として図2-5があります。
事象

 に対し、
に対し、










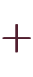










 が成り立つ。
が成り立つ。
「



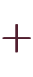



 」は
」は と
と の重複部分の確率が2回計上されているため、その部分の確率
の重複部分の確率が2回計上されているため、その部分の確率




 を引いたものが
を引いたものが




 と一致するイメージです。 例えば、「サイコロの
と一致するイメージです。 例えば、「サイコロの 以下または奇数が出る確率」
以下または奇数が出る確率」 「
「 以下が出る確率」
以下が出る確率」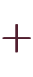 「奇数が出る確率」
「奇数が出る確率」 「
「 以下かつ奇数が出る確率」です。
以下かつ奇数が出る確率」です。







 」は
」は と
と の重複部分の確率が2回計上されているため、その部分の確率
の重複部分の確率が2回計上されているため、その部分の確率




 を引いたものが
を引いたものが




 と一致するイメージです。 例えば、「サイコロの
と一致するイメージです。 例えば、「サイコロの 以下または奇数が出る確率」
以下または奇数が出る確率」 「
「 以下が出る確率」
以下が出る確率」 「奇数が出る確率」
「奇数が出る確率」 「
「 以下かつ奇数が出る確率」です。
以下かつ奇数が出る確率」です。3確率変数と期待値
3.1確率変数
さて、ここからは標本に対して何らかの値が定まっているケースについて扱います。 例えば、サイコロを振って奇数が出たら

 円、偶数が出たら
円、偶数が出たら

 円のお金が貰えるとしたとき、標本に対して値を返す関数
円のお金が貰えるとしたとき、標本に対して値を返す関数 は図3-1のようになります。
は図3-1のようになります。


 円、偶数が出たら
円、偶数が出たら

 円のお金が貰えるとしたとき、標本に対して値を返す関数
円のお金が貰えるとしたとき、標本に対して値を返す関数 は図3-1のようになります。
は図3-1のようになります。標本空間













 と、標本
と、標本

 に対し、
に対し、






 のとき、
のとき、













 のとき、
のとき、







この のように、各標本に対して決まった実数を返す関数を、「確率変数」といいます。 名前に「変数」と付いていてややこしいですが、基本的に関数と考えてください。
のように、各標本に対して決まった実数を返す関数を、「確率変数」といいます。 名前に「変数」と付いていてややこしいですが、基本的に関数と考えてください。
 のように、各標本に対して決まった実数を返す関数を、「確率変数」といいます。 名前に「変数」と付いていてややこしいですが、基本的に関数と考えてください。
のように、各標本に対して決まった実数を返す関数を、「確率変数」といいます。 名前に「変数」と付いていてややこしいですが、基本的に関数と考えてください。3.2分布関数
一方、確率変数の値に対してそれが起こる確率を返す関数を、「分布関数」といい、それぞれの確率を「分布」といいます。 例えば「サイコロを振って奇数が出たら

 円、偶数が出たら
円、偶数が出たら

 円のお金が貰える」という場合、このときの分布関数を
円のお金が貰える」という場合、このときの分布関数を とすると、それぞれの分布は
とすると、それぞれの分布は















 となります。
となります。


 円、偶数が出たら
円、偶数が出たら

 円のお金が貰える」という場合、このときの分布関数を
円のお金が貰える」という場合、このときの分布関数を とすると、それぞれの分布は
とすると、それぞれの分布は















 となります。
となります。X軸を確率変数の値とし、Y軸を確率として、分布関数を図示すると、確率がどのように「分布」しているかが把握しやすくなります(図3-2)。
3.3期待値
それでは、「サイコロを振って奇数が出たら

 円、偶数が出たら
円、偶数が出たら

 円のお金が貰える」という例を考えた場合、いくらぐらい貰えそうだと「期待」することが妥当でしょうか。
円のお金が貰える」という例を考えた場合、いくらぐらい貰えそうだと「期待」することが妥当でしょうか。


 円、偶数が出たら
円、偶数が出たら

 円のお金が貰える」という例を考えた場合、いくらぐらい貰えそうだと「期待」することが妥当でしょうか。
円のお金が貰える」という例を考えた場合、いくらぐらい貰えそうだと「期待」することが妥当でしょうか。一つの方法としては、 の確率で
の確率で

 円が貰え、残りの
円が貰え、残りの の確率で
の確率で

 円が貰えるため、確率で重み付けした平均を計算して、
円が貰えるため、確率で重み付けした平均を計算して、












 円くらいだと考えることができそうです。
円くらいだと考えることができそうです。
 の確率で
の確率で

 円が貰え、残りの
円が貰え、残りの の確率で
の確率で

 円が貰えるため、確率で重み付けした平均を計算して、
円が貰えるため、確率で重み付けした平均を計算して、




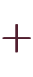








 円くらいだと考えることができそうです。
円くらいだと考えることができそうです。このような方法で計算される値を、「期待値」といいます。 別の例では、サイコロを振って、 以下が出たら
以下が出たら

 円、
円、 か
か が出たら
が出たら

 円、
円、 が出たら
が出たら

 円が貰えるとき、期待値は
円が貰えるとき、期待値は








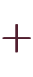









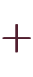












 円となります。
円となります。
 以下が出たら
以下が出たら

 円、
円、 か
か が出たら
が出たら

 円、
円、 が出たら
が出たら

 円が貰えるとき、期待値は
円が貰えるとき、期待値は








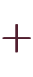





















 円となります。
円となります。これは図で表すと、第8回で説明した積分と同じであることが判ります(図3-3)。
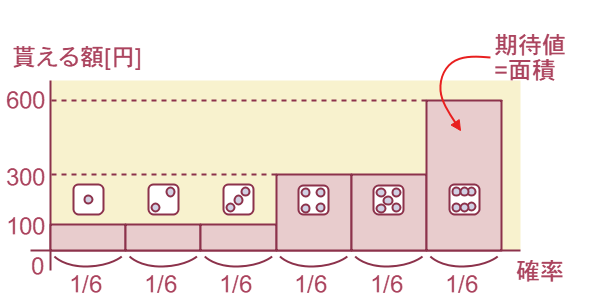
図のように、期待値は面積と考えることができます。 よって厳密には、期待値は図3-4のように積分を使って定義されています。
標本空間 、標本
、標本

 、確率変数
、確率変数 、確率
、確率 に対し、
に対し、













 のとき、期待値
のとき、期待値


 を
を














 と定義する。 また、
と定義する。 また、 が負にならない関数で
が負にならない関数で











 のとき、
のとき、




 と定義する。
と定義する。
数式はややこしいですが、確率で重み付けして面積を求めているだけです。 このように積分を使うことで、無限がかかわる場合にも計算できるようになります。
3.4分散
さて、「



 の確率で
の確率で




 円が貰え、それ以外では貰えない」という場合と、「必ず
円が貰え、それ以外では貰えない」という場合と、「必ず

 円貰える」という場合とでは、期待値は両方とも
円貰える」という場合とでは、期待値は両方とも

 円で同じですが、貰え方にはばらつきがあります。
円で同じですが、貰え方にはばらつきがあります。




 の確率で
の確率で




 円が貰え、それ以外では貰えない」という場合と、「必ず
円が貰え、それ以外では貰えない」という場合と、「必ず

 円貰える」という場合とでは、期待値は両方とも
円貰える」という場合とでは、期待値は両方とも

 円で同じですが、貰え方にはばらつきがあります。
円で同じですが、貰え方にはばらつきがあります。そこで、このばらつきを数式で表すことを考えます。 「期待値との差の二乗を平均したもの」で計算し、これを「分散」といいます。
例えば、「



 の確率で
の確率で




 円が貰え、それ以外では貰えない」場合の分散を計算すると、期待値は
円が貰え、それ以外では貰えない」場合の分散を計算すると、期待値は

 ですので、「平均する重み×期待値との差の二乗」を足して、「
ですので、「平均する重み×期待値との差の二乗」を足して、「










































 」となります。
」となります。




 の確率で
の確率で




 円が貰え、それ以外では貰えない」場合の分散を計算すると、期待値は
円が貰え、それ以外では貰えない」場合の分散を計算すると、期待値は

 ですので、「平均する重み×期待値との差の二乗」を足して、「
ですので、「平均する重み×期待値との差の二乗」を足して、「










































 」となります。
」となります。「必ず

 円貰える」場合の分散を計算すると、「
円貰える」場合の分散を計算すると、「












 」となります。
」となります。


 円貰える」場合の分散を計算すると、「
円貰える」場合の分散を計算すると、「












 」となります。
」となります。このように分散を計算することで、ばらつきの大きさが分かります。 数式で書くと、分散は図3-5のように定義されます。
確率変数 に対し、期待値
に対し、期待値 とすると、分散
とすると、分散


 を
を















 と定義する。
と定義する。
3.5大数の法則
「サイコロを振って6が出たら



 円、それ以外なら
円、それ以外なら

 円のお金が貰える」という場合を繰り返すと、
円のお金が貰える」という場合を繰り返すと、



 円が貰えたり
円が貰えたり

 円が貰えたりしますが、何度も繰り返すうちに貰えた額の平均は期待値の
円が貰えたりしますが、何度も繰り返すうちに貰えた額の平均は期待値の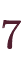

 円に近づいていくことが分かります。 実際に手元で
円に近づいていくことが分かります。 実際に手元で







 回試したところ、表3-1のようになりました。
回試したところ、表3-1のようになりました。




 円、それ以外なら
円、それ以外なら

 円のお金が貰える」という場合を繰り返すと、
円のお金が貰える」という場合を繰り返すと、



 円が貰えたり
円が貰えたり

 円が貰えたりしますが、何度も繰り返すうちに貰えた額の平均は期待値の
円が貰えたりしますが、何度も繰り返すうちに貰えた額の平均は期待値の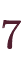

 円に近づいていくことが分かります。 実際に手元で
円に近づいていくことが分かります。 実際に手元で







 回試したところ、表3-1のようになりました。
回試したところ、表3-1のようになりました。| 回数 | 平均 |
|---|---|
 |
    |
  |
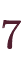   |
   |
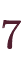   |
    |
     |
     |
      |
      |
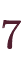       |
       |
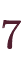        |
貰えた額の平均が期待値の「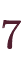

 」に近づくことが分かると思います。
」に近づくことが分かると思います。
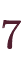

 」に近づくことが分かると思います。
」に近づくことが分かると思います。このように、試行回数を増やすと平均が期待値に近づくという現象を「大数の法則」といいます。
正確には「大数の法則」には2種類あり、多くのケースに適用できる「大数の弱法則」と、特定のケースにしか適用できない代わりにより強い形で表される「大数の強法則」があります。
「大数の弱法則」は図3-6のように定義されます。
確率変数の列










 とそれらの期待値
とそれらの期待値


 があり、任意の
があり、任意の

 に対して、
に対して、






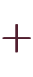


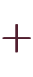

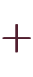















 が成り立つとき、「大数の弱法則」が成り立つという。
が成り立つとき、「大数の弱法則」が成り立つという。
式で表すと難しそうですが、平たく言うと大数の弱法則とは「試行を増やすと、平均と期待値に差がある確率が限りなく に近づく」ことを意味します。 つまり平均はどんどん期待値に近づくニュアンスですが、あくまで近づいているのはそうなるという確率である点に注意してください。
に近づく」ことを意味します。 つまり平均はどんどん期待値に近づくニュアンスですが、あくまで近づいているのはそうなるという確率である点に注意してください。
 に近づく」ことを意味します。 つまり平均はどんどん期待値に近づくニュアンスですが、あくまで近づいているのはそうなるという確率である点に注意してください。
に近づく」ことを意味します。 つまり平均はどんどん期待値に近づくニュアンスですが、あくまで近づいているのはそうなるという確率である点に注意してください。そこでもっと素直に「平均は限りなく期待値に近づく」と言えないかと考え、大数の強法則が現れました。 「大数の強法則」は図3-7のように定義されます。
確率変数の列










 とそれらの期待値
とそれらの期待値


 があり、
があり、





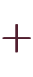


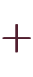

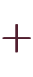












 が成り立つとき、「大数の強法則」が成り立つという。
が成り立つとき、「大数の強法則」が成り立つという。
平たく言うと大数の強法則とは「試行を増やすと平均が期待値に限りなく近づく確率が 」であることを意味します。
」であることを意味します。
 」であることを意味します。
」であることを意味します。そして「大数の弱法則」と「大数の強法則」は、それぞれ確率変数の列によって成り立ったり成り立たなかったりします。 成り立つことを示すために比較的よく使われる定理には、図3-8があります。
互いに独立で分布が同じ確率変数の列










 があり、いずれの分散も
があり、いずれの分散も でないとき、「大数の弱法則」が成り立つ。
でないとき、「大数の弱法則」が成り立つ。
例えば「サイコロを振って6が出たら



 円、それ以外なら
円、それ以外なら

 円のお金が貰える」という試行を何度も繰り返した場合を考えると、それぞれの試行は互いに独立で分布が同じで分散が有限なため、「大数の弱法則」が成り立ちます。 つまり、平均はどんどん期待値の
円のお金が貰える」という試行を何度も繰り返した場合を考えると、それぞれの試行は互いに独立で分布が同じで分散が有限なため、「大数の弱法則」が成り立ちます。 つまり、平均はどんどん期待値の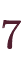

 円に近づく(そうならない確率が0に近づく)ことが数学的に言えます。
円に近づく(そうならない確率が0に近づく)ことが数学的に言えます。




 円、それ以外なら
円、それ以外なら

 円のお金が貰える」という試行を何度も繰り返した場合を考えると、それぞれの試行は互いに独立で分布が同じで分散が有限なため、「大数の弱法則」が成り立ちます。 つまり、平均はどんどん期待値の
円のお金が貰える」という試行を何度も繰り返した場合を考えると、それぞれの試行は互いに独立で分布が同じで分散が有限なため、「大数の弱法則」が成り立ちます。 つまり、平均はどんどん期待値の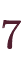

 円に近づく(そうならない確率が0に近づく)ことが数学的に言えます。
円に近づく(そうならない確率が0に近づく)ことが数学的に言えます。4統計学
ここまでは、標本空間が分かっているときに、そこから様々な確率や期待値などを計算してきました。
ここからは、標本空間が分からないときに、実際に起こったいくつかの標本から標本空間を推測する方法について説明します。
4.1母集団と標本
例えば、部品を製造している工場が不良品を作ってしまう確率を計算したいと考えた場合、正確には限りなく多い部品を製造してそのすべてをチェックする必要がありますが、現実には不可能なので製造した部品の一部をチェックしてそこから全体の確率を推測します。
このとき、最終的に推測したい全体を「母集団」と呼び、推測に使うためのいくつかのデータの集まりを「標本」と呼びます。 つまり例では、限りなく多い部品が「母集団」で、実際にチェックする部品が「標本」です。
そして標本から母集団を推測することを「推定」といい、母集団が直接調べられないときに様々な分野で活用されています。 普通は、標本は偏らないようにできるだけ無作為に選びます。
4.2平均と分散
母集団や標本を扱う分野では、期待値のことは「平均」と呼びます。 そして母集団における平均は「母平均」、標本における平均は「標本平均」といいます。
また、母集団における分散は「母分散」、標本における分散は「標本分散」といいます。
それでは、標本から母平均や母分散を推定してみましょう。
4.3点推定と区間推定
標本平均や標本分散から母平均や母分散を推定するには、「点推定」と「区間推定」の2つの方法があります。
「点推定」とは、標本平均や標本分散などの既知の値から、母集団の未知の値を推定する方法です。
標本の選ばれ方によって標本平均や標本分散にはばらつきが出てきます。 そこでそれら複数の標本に対し、「標本平均の平均」や「標本分散の平均」が母集団での値と一致するようにし、かつそれらの「標本平均の分散」や「標本分散の分散」が最小になるようにすると、母集団に近づいていきそうです。 このような式を作ると、最終的に図4-1の式が得られます。
標本の値を












 とし、それらの平均を
とし、それらの平均を 、分散を
、分散を


 とすると、母平均
とすると、母平均


 は
は




 で推定できる。 また母分散
で推定できる。 また母分散


 は
は

















 で推定できる。
で推定できる。
例えば、学校で



 人にテストを行ったとして、そこから無作為に
人にテストを行ったとして、そこから無作為に
 人分を抜き出して平均と分散を計算したところ、平均は
人分を抜き出して平均と分散を計算したところ、平均は
 点、分散は
点、分散は

 になったとします。 すると先ほどの式より、
になったとします。 すると先ほどの式より、



 人全員の平均は
人全員の平均は
 点、分散は
点、分散は

















 と推定できます。
と推定できます。




 人にテストを行ったとして、そこから無作為に
人にテストを行ったとして、そこから無作為に
 人分を抜き出して平均と分散を計算したところ、平均は
人分を抜き出して平均と分散を計算したところ、平均は
 点、分散は
点、分散は

 になったとします。 すると先ほどの式より、
になったとします。 すると先ほどの式より、



 人全員の平均は
人全員の平均は
 点、分散は
点、分散は

















 と推定できます。
と推定できます。この点推定に対し、「区間推定」とは、未知の母集団の値がどの区間にあるかを推定する方法です。 既知の標本の値と、自由に決めた「信頼度」という値を元に、母集団の値が存在しそうな区間が得られます。 信頼度が高いほど得られた区間に母集団の値が入る確率が高くなりますが、区間の幅も大きくなります。
例えば、無作為に選んだ
 人分のテストの結果から、信頼度を
人分のテストの結果から、信頼度を


 として学校全体での平均点を区間推定すると、
として学校全体での平均点を区間推定すると、


 点以上
点以上


 点以下などの区間が得られるというイメージです。 この場合、信頼度で与えた
点以下などの区間が得られるというイメージです。 この場合、信頼度で与えた


 の確率で、母平均がこの区間にあることを意味します。
の確率で、母平均がこの区間にあることを意味します。

 人分のテストの結果から、信頼度を
人分のテストの結果から、信頼度を


 として学校全体での平均点を区間推定すると、
として学校全体での平均点を区間推定すると、


 点以上
点以上


 点以下などの区間が得られるというイメージです。 この場合、信頼度で与えた
点以下などの区間が得られるというイメージです。 この場合、信頼度で与えた


 の確率で、母平均がこの区間にあることを意味します。
の確率で、母平均がこの区間にあることを意味します。また推定のほかにも、標本をもとにある結論が言えるかどうかを判断する方法として「検定」というものもあります。 例えば、「コインを
 回投げると
回投げると 回が表だったとき、これは偶然ではなくコインが歪んでいると言えるか」といった場面で検定が使えます。
回が表だったとき、これは偶然ではなくコインが歪んでいると言えるか」といった場面で検定が使えます。

 回投げると
回投げると 回が表だったとき、これは偶然ではなくコインが歪んでいると言えるか」といった場面で検定が使えます。
回が表だったとき、これは偶然ではなくコインが歪んでいると言えるか」といった場面で検定が使えます。今回は、確率について説明しました。 次回は、複数の数をひとまとめにする「ベクトル」と「行列」について解説します!