1リーマン積分
第7話では「微分」を「接線の傾きを求める方法」と説明しました。 これに対して今回解説する「積分」は「面積を求める方法」と言えます。
さて、まずは図1-1のような問題を考えてみましょう。
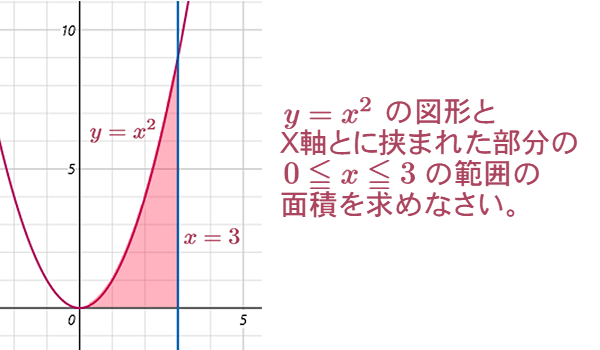
このような面積も、第7話で行った方法と同様に「極限」を使うことで求まります。
1.1リーマン和
この問題を解くにはまず、面積を求めたい領域を縦にいくつかの区間に分割します(図1-2)。
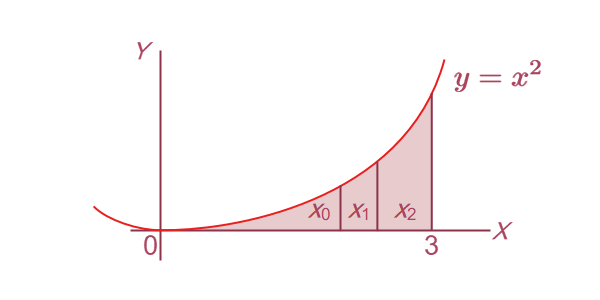
この例では、 が
が から
から の間を
の間を






 の3つの領域に区切りました。
の3つの領域に区切りました。
 が
が から
から の間を
の間を






 の3つの領域に区切りました。
の3つの領域に区切りました。次に、それぞれの区間の中で


 上の点を自由に選んで長方形を作ります(図1-3)。
上の点を自由に選んで長方形を作ります(図1-3)。



 上の点を自由に選んで長方形を作ります(図1-3)。
上の点を自由に選んで長方形を作ります(図1-3)。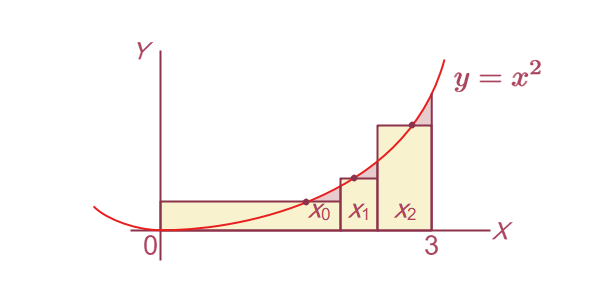
ちなみに、このように作った長方形の面積の合計を「リーマン和」と呼びます。
1.2リーマン積分
ここで、
 から
から
 を使って3つの領域に分割していた区間を、もっと細かく、例えば
を使って3つの領域に分割していた区間を、もっと細かく、例えば
 から
から

 の100個の領域のように分割していくと、直感的にはこのリーマン和が本来求めたかった面積に近づいていくことが解ると思います(図1-4)。
の100個の領域のように分割していくと、直感的にはこのリーマン和が本来求めたかった面積に近づいていくことが解ると思います(図1-4)。

 から
から
 を使って3つの領域に分割していた区間を、もっと細かく、例えば
を使って3つの領域に分割していた区間を、もっと細かく、例えば
 から
から

 の100個の領域のように分割していくと、直感的にはこのリーマン和が本来求めたかった面積に近づいていくことが解ると思います(図1-4)。
の100個の領域のように分割していくと、直感的にはこのリーマン和が本来求めたかった面積に近づいていくことが解ると思います(図1-4)。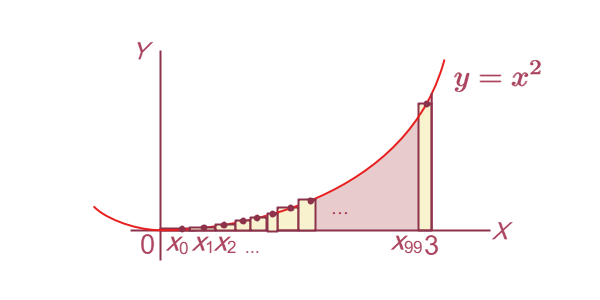
そして、区間をどのように分割しても、区間が細かくなるように分割数を限りなく増やしていくとリーマン和が同じ値に収束するならば、この値を「リーマン積分」といい、図形の面積と一致します。
1.3具体的な値
それでは具体的に先ほどの図形の面積の値を求めてみましょう。
先ほどリーマン積分の定義で「区間をどのように分割しても」と言いましたが、実際にあらゆる分割方法を検証することは困難ですので、「ダルブーの定理」と呼ばれる定理が使われます。
この定理の一部を解りやすく言い換えると図1-5のようになります。
 が有界(取りうる値が一定の範囲に収まっている)な関数で、
が有界(取りうる値が一定の範囲に収まっている)な関数で、 のある分割に対して区間が細かくなるように分割数を増やしたとき、リーマン和が最大になるときとリーマン和が最小になるときとで同じ値に収束するならば、この値はリーマン積分と一致する。
のある分割に対して区間が細かくなるように分割数を増やしたとき、リーマン和が最大になるときとリーマン和が最小になるときとで同じ値に収束するならば、この値はリーマン積分と一致する。
要するに、この定理を使うと分割方法の1つを検証するだけでリーマン積分が可能となるわけです。
ここでは計算を簡単にするために、分割方法を等分割にしておきます。 先ほどの問題に対し、等分割したリーマン和が最大の場合と最小の場合を考えて、それぞれの極限を求めると図1-6のようになります。
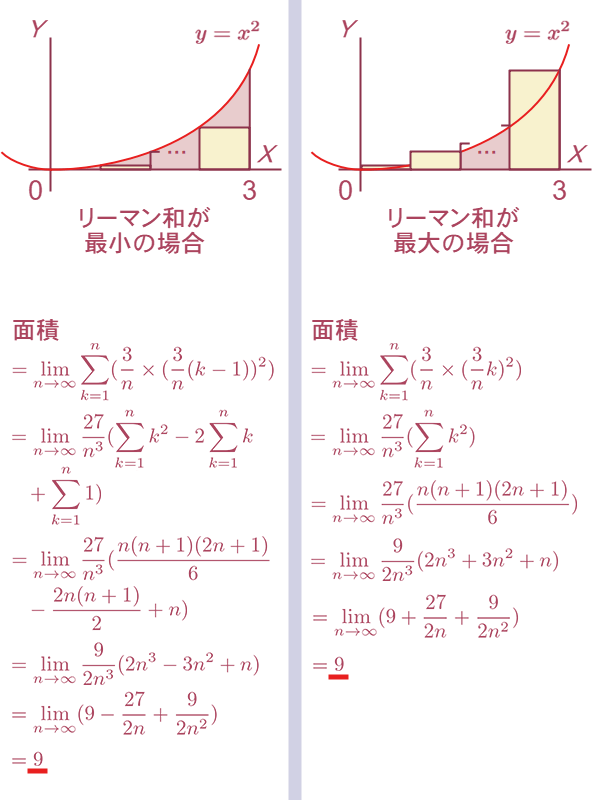
最大の場合と最小の場合において、分割を限りなく大きくしていくとリーマン和は同じ値「 」に近づくことが判ったため、ダルブーの定理より、この値はリーマン積分と一致します。 よって、求めたい面積の答えは「
」に近づくことが判ったため、ダルブーの定理より、この値はリーマン積分と一致します。 よって、求めたい面積の答えは「 」です。
」です。
 」に近づくことが判ったため、ダルブーの定理より、この値はリーマン積分と一致します。 よって、求めたい面積の答えは「
」に近づくことが判ったため、ダルブーの定理より、この値はリーマン積分と一致します。 よって、求めたい面積の答えは「 」です。
」です。2不定積分と逆微分
さて、毎回このようにリーマン積分を求めるのは大変ですので、第7話の微分のときと同様に、主な関数についてリーマン積分した結果だけを紹介します。
先ほどは

 から
から

 の区間でリーマン積分を求めましたが、任意の区間で求まったほうが便利なため、変数
の区間でリーマン積分を求めましたが、任意の区間で求まったほうが便利なため、変数

 に対し、
に対し、

 から
から

 の区間に一般化したリーマン積分を求めることにします。
の区間に一般化したリーマン積分を求めることにします。


 から
から

 の区間でリーマン積分を求めましたが、任意の区間で求まったほうが便利なため、変数
の区間でリーマン積分を求めましたが、任意の区間で求まったほうが便利なため、変数

 に対し、
に対し、

 から
から

 の区間に一般化したリーマン積分を求めることにします。
の区間に一般化したリーマン積分を求めることにします。ちなみに、このように任意の区間に一般化して図形


 の面積が求まるようにすることを「不定積分」といい、
の面積が求まるようにすることを「不定積分」といい、





 と書きます。 これに対し、先ほどの
と書きます。 これに対し、先ほどの

 から
から

 の区間のように、具体的な区間で図形
の区間のように、具体的な区間で図形


 の面積を求めることを「定積分」といい、
の面積を求めることを「定積分」といい、





 のように書きます。
のように書きます。



 の面積が求まるようにすることを「不定積分」といい、
の面積が求まるようにすることを「不定積分」といい、





 と書きます。 これに対し、先ほどの
と書きます。 これに対し、先ほどの

 から
から

 の区間のように、具体的な区間で図形
の区間のように、具体的な区間で図形


 の面積を求めることを「定積分」といい、
の面積を求めることを「定積分」といい、





 のように書きます。
のように書きます。





 という書き方は独特ですが、「
という書き方は独特ですが、「 」とは
」とは から
から の区間において足し合わせることを表し、「
の区間において足し合わせることを表し、「
 」とは微分のときにも現れましたが限りなく微小な
」とは微分のときにも現れましたが限りなく微小な を表します。 つまり「
を表します。 つまり「





 」とは、高さ
」とは、高さ


 と幅
と幅
 を掛けて得られる細長い長方形の面積を、
を掛けて得られる細長い長方形の面積を、

 から
から

 の区間において足し合わせたものというニュアンスです。 先ほど計算した通り、
の区間において足し合わせたものというニュアンスです。 先ほど計算した通り、





 です。
です。一方、不定積分





 とは、任意の区間「
とは、任意の区間「

 から
から

 」に対して「
」に対して「















 」が成り立つような
」が成り立つような










 のことと定義されます。 つまり、このような関数
のことと定義されます。 つまり、このような関数


 が見つかれば、毎回リーマン和の極限を計算しなくても
が見つかれば、毎回リーマン和の極限を計算しなくても







 で面積が求まるというわけです。
で面積が求まるというわけです。






 とは、任意の区間「
とは、任意の区間「

 から
から

 」に対して「
」に対して「















 」が成り立つような
」が成り立つような










 のことと定義されます。 つまり、このような関数
のことと定義されます。 つまり、このような関数


 が見つかれば、毎回リーマン和の極限を計算しなくても
が見つかれば、毎回リーマン和の極限を計算しなくても







 で面積が求まるというわけです。
で面積が求まるというわけです。さっそくこの不定積分を見ていきましょう。
2.1不定積分
先ほどの


 の関数に対して不定積分を行うと、結論から言うと「
の関数に対して不定積分を行うと、結論から言うと「














 」になります。
」になります。  は任意の定数で、どのような数が代入されても成り立つというものです。
は任意の定数で、どのような数が代入されても成り立つというものです。



 の関数に対して不定積分を行うと、結論から言うと「
の関数に対して不定積分を行うと、結論から言うと「














 」になります。
」になります。  は任意の定数で、どのような数が代入されても成り立つというものです。
は任意の定数で、どのような数が代入されても成り立つというものです。例えばこれを

 から
から

 の区間で計算すると、「
の区間で計算すると、「

































 」となり、確かに先ほどの結果と一致します。 単に引き算
」となり、確かに先ほどの結果と一致します。 単に引き算







 を計算しただけです。
を計算しただけです。


 から
から

 の区間で計算すると、「
の区間で計算すると、「

































 」となり、確かに先ほどの結果と一致します。 単に引き算
」となり、確かに先ほどの結果と一致します。 単に引き算







 を計算しただけです。
を計算しただけです。また

 から
から

 の区間の場合も、「
の区間の場合も、「

































 」のようにリーマン和の極限を計算することなく、引き算で簡単に求まります。
」のようにリーマン和の極限を計算することなく、引き算で簡単に求まります。


 から
から

 の区間の場合も、「
の区間の場合も、「

































 」のようにリーマン和の極限を計算することなく、引き算で簡単に求まります。
」のようにリーマン和の極限を計算することなく、引き算で簡単に求まります。2.2逆微分
さてこの不定積分の関数はどうすれば求まるかについてですが、関数が連続している場合、実は微分の逆操作で求めることができます。 つまり、








 のとき、
のとき、










 です。
です。









 のとき、
のとき、










 です。
です。例えば
 の不定積分を求めたい場合、微分して
の不定積分を求めたい場合、微分して
 になる関数を探すと「
になる関数を探すと「









 」のため、「
」のため、「



 」が不定積分の結果となります。
」が不定積分の結果となります。

 の不定積分を求めたい場合、微分して
の不定積分を求めたい場合、微分して
 になる関数を探すと「
になる関数を探すと「









 」のため、「
」のため、「



 」が不定積分の結果となります。
」が不定積分の結果となります。つまり、関数が連続している場合、微分して


 になるような関数
になるような関数


 を見つけることが、
を見つけることが、


 を不定積分することになります。 このような関数
を不定積分することになります。 このような関数


 を「原始関数」といいます。
を「原始関数」といいます。



 になるような関数
になるような関数


 を見つけることが、
を見つけることが、


 を不定積分することになります。 このような関数
を不定積分することになります。 このような関数


 を「原始関数」といいます。
を「原始関数」といいます。2.3主な関数の不定積分
主な関数の不定積分は表2-1の通りです。
| 関数 | 原始関数 |
|---|---|
    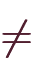    |
       |
 |
        |
    |
       |
    |
      |
  |
    |
これらの使い方としては、例えば定積分の「





 」を求めたい場合、表にある不定積分の「
」を求めたい場合、表にある不定積分の「


















 」を使って、「
」を使って、「





































 」のように求まります。
」のように求まります。






 」を求めたい場合、表にある不定積分の「
」を求めたい場合、表にある不定積分の「


















 」を使って、「
」を使って、「





































 」のように求まります。
」のように求まります。これらの不定積分の結果はいずれも、微分すると元の関数に戻ることが分かります。 例えば一番上の「





 」を微分すると、
」を微分すると、






















 となり、元の関数「
となり、元の関数「
 」になります。
」になります。






 」を微分すると、
」を微分すると、






















 となり、元の関数「
となり、元の関数「
 」になります。
」になります。3広義リーマン積分
さて次に、リーマン積分ができない例として、図3-1の問題を考えてみましょう。
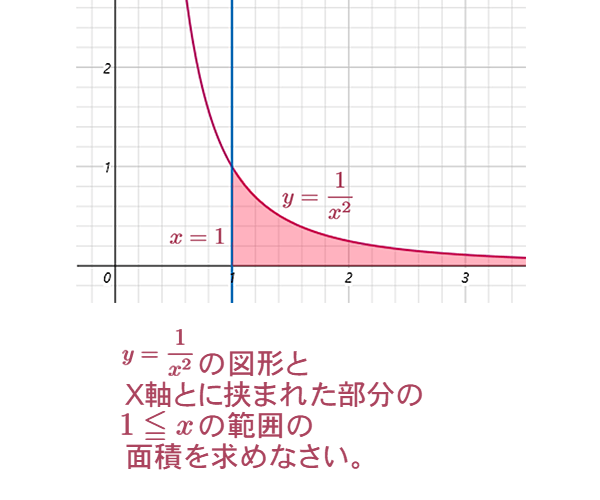
この場合、図形は右にどこまでも続いていて、区間が有限でないためリーマン和が作れず、リーマン積分ができません。
そこでどうするかというと、任意の

 から
から

 の区間で計算できる不定積分を用いて、その区間を限りなく広げて極限を使ってリーマン積分を拡張することを考えます。 つまりこの問題は、
の区間で計算できる不定積分を用いて、その区間を限りなく広げて極限を使ってリーマン積分を拡張することを考えます。 つまりこの問題は、


















 と考えます。
と考えます。


 から
から

 の区間で計算できる不定積分を用いて、その区間を限りなく広げて極限を使ってリーマン積分を拡張することを考えます。 つまりこの問題は、
の区間で計算できる不定積分を用いて、その区間を限りなく広げて極限を使ってリーマン積分を拡張することを考えます。 つまりこの問題は、


















 と考えます。
と考えます。このように、極限を使って拡張したリーマン積分を、「広義リーマン積分」といいます。
こうすることで図3-2のように計算することができます。



 を不定積分すると、
を不定積分すると、
















 なので、
なので、
広義リーマン積分より、













































よって答えは、「 」になります。
」になります。
 」になります。
」になります。4重積分
リーマン積分を多変数に拡張することで、立体の体積などを求めることもできます。
例えば、立体の方程式




 に対し、
に対し、

 から
から

 、
、

 から
から

 の区間の体積は、この区間を
の区間の体積は、この区間を として
として









 と書きます。 これまでの方法と同様に、この立体に対して分割してリーマン和の極限を求めることで、この立体の体積が求まります。
と書きます。 これまでの方法と同様に、この立体に対して分割してリーマン和の極限を求めることで、この立体の体積が求まります。





 に対し、
に対し、

 から
から

 、
、

 から
から

 の区間の体積は、この区間を
の区間の体積は、この区間を として
として









 と書きます。 これまでの方法と同様に、この立体に対して分割してリーマン和の極限を求めることで、この立体の体積が求まります。
と書きます。 これまでの方法と同様に、この立体に対して分割してリーマン和の極限を求めることで、この立体の体積が求まります。このように、多変数に対して行う積分を「重積分」と言います。
そして、積分する関数が有界(取りうる値が一定の範囲に収まっている)かつ、多変数



 のそれぞれの区間も有界のとき、この重積分は一変数の積分の組み合わせに直すことができます。 例えば、
のそれぞれの区間も有界のとき、この重積分は一変数の積分の組み合わせに直すことができます。 例えば、






















 とできます。 あとは内側から、これまでのようにリーマン積分を計算すると体積が求まります。
とできます。 あとは内側から、これまでのようにリーマン積分を計算すると体積が求まります。




 のそれぞれの区間も有界のとき、この重積分は一変数の積分の組み合わせに直すことができます。 例えば、
のそれぞれの区間も有界のとき、この重積分は一変数の積分の組み合わせに直すことができます。 例えば、






















 とできます。 あとは内側から、これまでのようにリーマン積分を計算すると体積が求まります。
とできます。 あとは内側から、これまでのようにリーマン積分を計算すると体積が求まります。5測度とルベーグ積分
さて、ここまでユークリッド空間の連続した図形に対して面積や体積を求めてきましたが、曲がった空間や不連続な図形を考えるとこれまでの方法では求まらないことがあります。 またさらに一般の集合を考えると、そもそも長さや面積の定義が自明ではないため、どのような長さに対しても面積が求まるようにしたほうが便利です。
そこで、長さや面積や体積を一般化して「測度」というものを集合に定義し、その測度における積分を求める「ルベーグ積分」というものが生まれました。
ルベーグ積分は、より多くのものに対して積分できるように、やや回りくどいですが図5-1の流れで行います。
- ルベーグ積分したい対象を含む集合
 に対し、そもそも測れるようにするためのルール「
に対し、そもそも測れるようにするためのルール「 -加法族」を導入する。
-加法族」を導入する。 - この
 -加法族の上に、実際の測り方を定義する。 この測り方を「測度」という。
-加法族の上に、実際の測り方を定義する。 この測り方を「測度」という。  における
における -加法族を
-加法族を とし、
とし、 上の測度を
上の測度を とすると、これらをセットにした
とすると、これらをセットにした





 を「測度空間」という。
を「測度空間」という。- 任意の測度空間上の関数に対し、「ルベーグ積分」を行う。
この(1)から(4)を図で表すと図5-2のようになります。
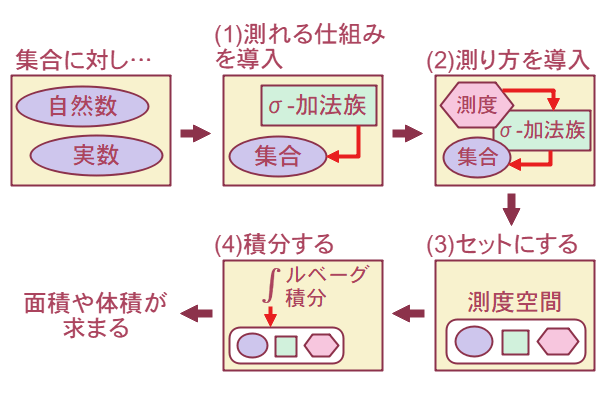
このような流れにすることで、「測度空間」さえ作れば、どのようなものでも積分できるようになります。 例えば図形や立体に限らず、「確率」といったものも積分できます。 このため、現代の確率論はルベーグ積分をベースに構築されています。
ちなみにユークリッド空間を対象とする場合、今までわたしたちが面積や体積や長さとして考えていたものをそのまま自然に拡張した「ルベーグ測度」という測度がよく使われます。 また、このときの -加法族として「ボレル集合体」と呼ばれるものがよく使われます。
-加法族として「ボレル集合体」と呼ばれるものがよく使われます。
 -加法族として「ボレル集合体」と呼ばれるものがよく使われます。
-加法族として「ボレル集合体」と呼ばれるものがよく使われます。では、具体的にルベーグ積分の問題を解いてみましょう(図5-3)。
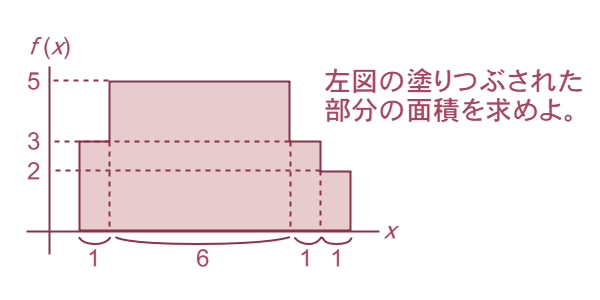
あえて変な測り方をする必要はないため、ここでは2次元ユークリッド空間とし、ボレル集合体とルベーグ測度を使った測度空間を仮定します。
ざっくりというと、リーマン積分は図形を縦に分割して面積を求める方法でした。 これに対し、ルベーグ積分は横に分割して面積を求める方法と言えます。
一般的なルベーグ積分の定義はやや複雑ですが、関数


 の取り得る値が有限個かつ負でないとき、ルベーグ積分は図5-4のように定義されます。
の取り得る値が有限個かつ負でないとき、ルベーグ積分は図5-4のように定義されます。



 の取り得る値が有限個かつ負でないとき、ルベーグ積分は図5-4のように定義されます。
の取り得る値が有限個かつ負でないとき、ルベーグ積分は図5-4のように定義されます。測度空間





 上の関数
上の関数


 に対し、
に対し、


 の値域が
の値域が






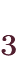




 の有限個でかつ負でないとき、それぞれに対する
の有限個でかつ負でないとき、それぞれに対する を
を






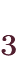




 とすると、
とすると、 全体でのルベーグ積分
全体でのルベーグ積分









 は、
は、


















 と定義される。
と定義される。
要するに、ある数 に対し、
に対し、


 が
が となるときの
となるときの を集めてその
を集めてその がどのくらいあるか(測度)を求め、
がどのくらいあるか(測度)を求め、 とその測度を掛けたものが面積の一部になるという流れです。
とその測度を掛けたものが面積の一部になるという流れです。
 に対し、
に対し、


 が
が となるときの
となるときの を集めてその
を集めてその がどのくらいあるか(測度)を求め、
がどのくらいあるか(測度)を求め、 とその測度を掛けたものが面積の一部になるという流れです。
とその測度を掛けたものが面積の一部になるという流れです。この方法を先ほどの問題に適用して解くと、図5-5のようになります。
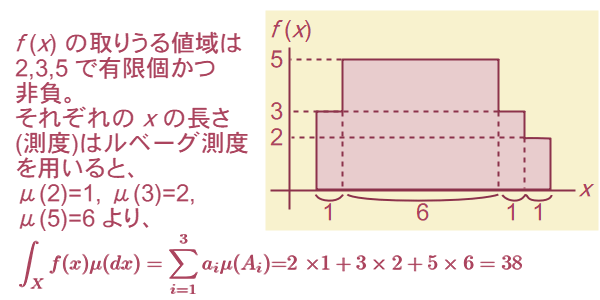
この例では非常に簡単な面積を求めましたが、例えばすべての点で不連続な関数など、直感的には面積が分からない関数でもルベーグ積分を使えば求められる強みがあります。
今回は、図形の面積を求める「積分」について説明しました。 次回は、この積分の上に構築した「確率」と「統計」について解説します!