3ページ目
サイコロで1～10を作る

1～10の乱数が欲しいことは多々ありますので、挑戦してみましょう！

まず、サイコロ1つを1回だけ振って、1～10の乱数が作れるかを考えてみます。 これは1～6の目を1～10の乱数に対応付けることになるため、目のパターンが足りず不可能であることが分かります(図1-1)。

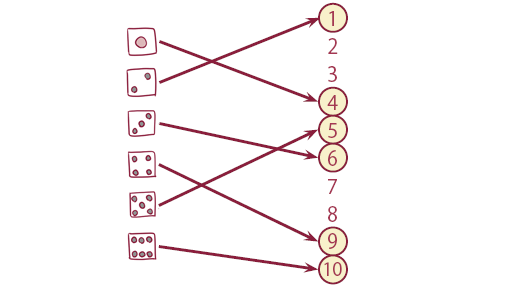
従って、サイコロを2つ以上使うか、2回以上振る必要があります。

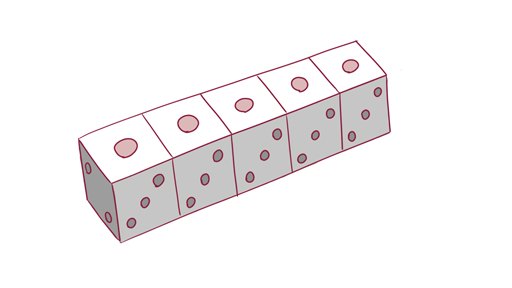
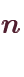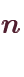では、サイコロを2つ以上、もしくは2回以上振って、ちょうど1～10の乱数に均等に対応させることはできるでしょうか。 サイコロを回振ったとき、出る目のパターンは通りになります。 しかし、6を何乗しても一の位は6のままですので、1～10に対応させようとすると常に6余ります(図1-2)。

よって、これらのパターンを1～10の乱数に均等に対応させることは不可能です。

一つの対処策としては、余った6パターンが出たときにサイコロをもう一度振ることが考えられます。 例えばサイコロを2回振り、1回目に6が出たらもう一度振り直すとします。 このとき図1-3のようなパターンで割り振ると、1～10の乱数になります。

このように余った6パターンをもう一度振り直すことで、1～10の乱数が作れます。 ただしこの場合、6/36の確率でサイコロを振り直さなければならないので、運が悪ければ無限にサイコロを振る羽目になります。

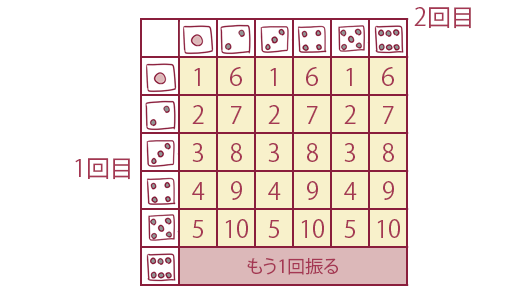
別の方法として無限級数の和を用いる方法も考えられます。 目の合計が9以外になるまで2個のサイコロを振り続けると、サイコロを振った回数が偶数になる確率は、なんと1/10となります(図2-1)。

ただこの方法で1/10の確率を作り出すことはできますが、このままでは1～10の乱数にはなりません。 そこで1/10が出なければ同様に、1/9、1/8、1/7、…の確率を作り出すことで、結果的に1～10の乱数を等しい確率で生成することができます(図2-2)。

しかし明らかに煩雑な上、振り直す回数も多くなるので、この方法は有用ではなさそうです。

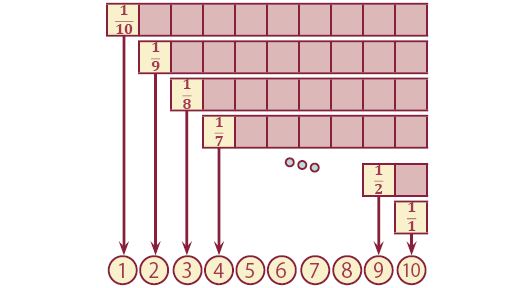
複数のサイコロを接着剤で接合させることで、物理的に1～10が作れないかを考えてみました。

が、思いつきませんでした(図3-1)。

結局、これが一番良さそうです(図4-1)。