2025年09月16日くいなちゃん
トランプのゲーム「神経衰弱」には、わざとミスしたほうが良い場面があることを検証します。
1神経衰弱の勝率
2人で遊ぶトランプのゲーム「神経衰弱」とは、ご存じの通り、裏返された2枚のカードをめくって同じ数字なら取得でき、違う数字なら裏に戻して相手の番になるというルールの、プレイヤーの記憶力が試されるゲームです。
多くの人は、図1-1の戦術で遊んでいるのではないでしょうか。
- 一度めくられた中に同じ数字が存在すれば、その2枚を選ぶ。
- なければ、一度もめくられていないカードを1枚選ぶ。
- 1枚選んだカードと同じ数字が、一度めくられた中に存在すれば、それを選ぶ。
- なければ、めくられていない中から選ぶ。
実は、記憶力の良い両者がこの戦術をとると、先手と後手で勝率に大きな差ができます。 以下で見ていきましょう。
1.12枚の場合
両者とも記憶力が十分良く、絶対に忘れない場合、神経衰弱は単に確率のゲームとみなせます。 先ほどの戦術を使うこととして、両者の勝率を求めてみます。 2枚で神経衰弱を行う場合、先手がその2枚を選ぶので、明らかに先手が100%勝ちます(図1-2)。
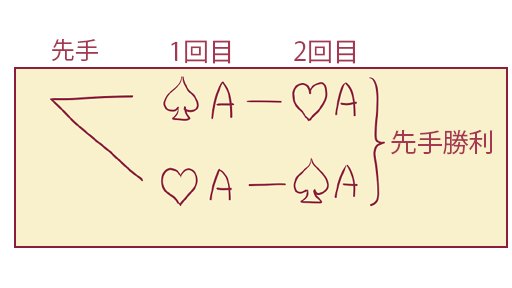
この例ではスペードとハートのカードを使っています。 先手が1回目に「スペードのA」を引いて2回目に「ハートのA」を引くパターンと、1回目に「ハートのA」を引いて2回目に「スペードのA」を引くパターンがありますが、どちらも先手の勝利です。
1.24枚の場合
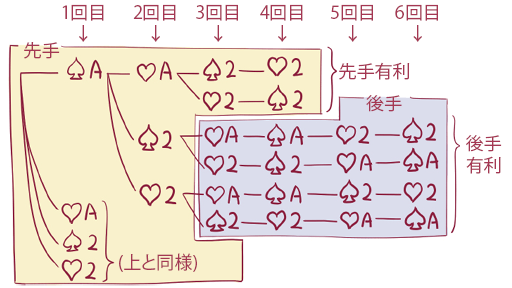
4枚で神経衰弱を行う場合は、起こりうる全パターンを網羅してみると、結果的に先手の勝率は1/3、後手は2/3となります(図1-3)。
1.312枚までの勝率
6枚の場合は、起こりうるパターン数が増えて計算が複雑ですが、先手の勝率は7/15、後手は8/15でした。 以後、地道に計算した結果、12枚までの勝率は表1-1のようになりました。
| 枚数 | 先手の勝率 | 後手の勝率 | 引き分け |
|---|---|---|---|
| 2 | 100.00% | 0.00% | 0.00% |
| 4 | 33.33% | 66.67% | 0.00% |
| 6 | 46.67% | 53.33% | 0.00% |
| 8 | 60.00% | 26.67% | 13.33% |
| 10 | 45.40% | 54.60% | 0.00% |
| 12 | 36.82% | 50.83% | 12.35% |
このように、枚数によって先手と後手の勝率に大きな差があることが確認できます。 これ以上枚数が増えると勝率の計算が大変になりますが、枚数が増えるにつれ勝率は50%ずつに近づいていきます。
2神経衰弱でわざとミスすべき場面
さてここで、わざとミスする戦術を考えてみましょう(図2-1)。
- 一度めくられた中に同じ数字が存在すれば、その2枚を選ぶ。
- なければ、一度もめくられていないカードを1枚選ぶ。
- 1枚選んだカードと同じ数字が、一度めくられた中に存在すれば、それを選ぶ。
- なければ、既にめくられたカードを選んでわざとミスする。
最初の戦術と異なるのは、最後の部分だけです。 闇雲にカードを開くと相手にヒントを与えることになるため、わざとミスすることで順番を相手に渡す(=パスする)という戦術です。
最初の戦術を「戦術A」と呼び、わざとミスをするというこの戦術を「戦術B」と呼びましょう。 既にめくられたカードがなければパスできませんが、話を単純にするために常にパスできるというルールで、12枚での勝率を計算した結果が表2-1です。
| 先手の戦術 | 後手の戦術 | 先手の勝率 | 後手の勝率 | 引き分け |
|---|---|---|---|---|
| 戦術A | 戦術A | 36.82% | 50.83% | 12.35% |
| 戦術A | 戦術B | 54.38% | 31.52% | 14.10% |
| 戦術B | 戦術A | 50.09% | 37.27% | 12.64% |
| 戦術B | 戦術B | 19.35% | 66.22% | 14.43% |
両者が戦術Aをとった場合には先手の勝率が36.82%しかありませんでしたが、先手がわざとミスをすることで勝率を50.09%まで上げることができています。
3結論
神経衰弱をするカードの枚数によっては、わざとミスしたほうが勝率が上がる場合があることが確認できました。