1複素数
1.1複素数
では「



 」を満たす
」を満たす はどうでしょうか。 先ほどと同様に考えると、
はどうでしょうか。 先ほどと同様に考えると、 は
は 乗すると「
乗すると「
 」になる数であって、「
」になる数であって、「

 」と「
」と「


 」の2つの数となります。 しかしすべての実数は
」の2つの数となります。 しかしすべての実数は 乗すると
乗すると 以上になるため、
以上になるため、 乗すると
乗すると
 となる数「
となる数「 」は、実数ではありません。
」は、実数ではありません。




 」を満たす
」を満たす はどうでしょうか。 先ほどと同様に考えると、
はどうでしょうか。 先ほどと同様に考えると、 は
は 乗すると「
乗すると「
 」になる数であって、「
」になる数であって、「

 」と「
」と「


 」の2つの数となります。 しかしすべての実数は
」の2つの数となります。 しかしすべての実数は 乗すると
乗すると 以上になるため、
以上になるため、 乗すると
乗すると
 となる数「
となる数「 」は、実数ではありません。
」は、実数ではありません。この「 」を数として認めるかどうかは、歴史的に議論がありました。 そして最終的にはこの「
」を数として認めるかどうかは、歴史的に議論がありました。 そして最終的にはこの「 」を実数全体の集合
」を実数全体の集合 に加えた、新しい数の集合が生まれました。 この数を「複素数」といい、複素数全体の集合をよく
に加えた、新しい数の集合が生まれました。 この数を「複素数」といい、複素数全体の集合をよく で表します。
で表します。
 」を数として認めるかどうかは、歴史的に議論がありました。 そして最終的にはこの「
」を数として認めるかどうかは、歴史的に議論がありました。 そして最終的にはこの「 」を実数全体の集合
」を実数全体の集合 に加えた、新しい数の集合が生まれました。 この数を「複素数」といい、複素数全体の集合をよく
に加えた、新しい数の集合が生まれました。 この数を「複素数」といい、複素数全体の集合をよく で表します。
で表します。複素数全体の集合 には、実数全体と
には、実数全体と のほかに、
のほかに、 の実数倍や、それらの和も含まれます。 例えば「
の実数倍や、それらの和も含まれます。 例えば「 」や「
」や「
 」や「
」や「


 」も
」も の元です。
の元です。
 には、実数全体と
には、実数全体と のほかに、
のほかに、 の実数倍や、それらの和も含まれます。 例えば「
の実数倍や、それらの和も含まれます。 例えば「 」や「
」や「
 」や「
」や「


 」も
」も の元です。
の元です。また、この「 」は「虚数単位」と呼ばれ、よく「
」は「虚数単位」と呼ばれ、よく「 」の記号で表されます。 つまり複素数とは、実数
」の記号で表されます。 つまり複素数とは、実数

 に対し「
に対し「


 」と書ける数だといえます(図1-1)。
」と書ける数だといえます(図1-1)。
 」は「虚数単位」と呼ばれ、よく「
」は「虚数単位」と呼ばれ、よく「 」の記号で表されます。 つまり複素数とは、実数
」の記号で表されます。 つまり複素数とは、実数

 に対し「
に対し「


 」と書ける数だといえます(図1-1)。
」と書ける数だといえます(図1-1)。任意の実数

 に対し「
に対し「


 」と表されるもの全体の集合を、複素数全体の集合
」と表されるもの全体の集合を、複素数全体の集合 と定義する。 また
と定義する。 また の元を「複素数」と呼ぶ。
の元を「複素数」と呼ぶ。
1.2複素数の有用性
なぜ「 」のような、よく分からない数を扱おうとするかといいますと、利点は2つあります。
」のような、よく分からない数を扱おうとするかといいますと、利点は2つあります。
 」のような、よく分からない数を扱おうとするかといいますと、利点は2つあります。
」のような、よく分からない数を扱おうとするかといいますと、利点は2つあります。1つは、最終的に実数が得られる計算であっても、計算の途中に複素数が現れることがあり、計算する上で避けられないことがあるからです。 例えば三次方程式「












 」の解の公式(代数的な)を作り出すと、解がすべて実数だったとしても、式中に複素数が出てくることは避けられないことが証明されています。
」の解の公式(代数的な)を作り出すと、解がすべて実数だったとしても、式中に複素数が出てくることは避けられないことが証明されています。













 」の解の公式(代数的な)を作り出すと、解がすべて実数だったとしても、式中に複素数が出てくることは避けられないことが証明されています。
」の解の公式(代数的な)を作り出すと、解がすべて実数だったとしても、式中に複素数が出てくることは避けられないことが証明されています。もう1つは、複素数の掛け算がちょうど回転操作になっていることから、幾何ベクトルを回転行列で操作するよりも簡潔に回転操作が表せるという応用上の利点があります。 周期的な波も回転で表すことができ、波を扱う電気の交流回路や音の波形処理などでも使われます。
1.3基本的な演算
2つの複素数「


 」と「
」と「


 」には、加算、減算、乗算、除算が定義されます。
」には、加算、減算、乗算、除算が定義されます。



 」と「
」と「


 」には、加算、減算、乗算、除算が定義されます。
」には、加算、減算、乗算、除算が定義されます。加算と減算は、

 であることを考えると自然に定義でき、加算は「
であることを考えると自然に定義でき、加算は「
























 」、減算は「
」、減算は「
























 」となります。 例えば、
」となります。 例えば、
















 です。
です。


 であることを考えると自然に定義でき、加算は「
であることを考えると自然に定義でき、加算は「
























 」、減算は「
」、減算は「
























 」となります。 例えば、
」となります。 例えば、
















 です。
です。乗算も、括弧を展開することで「












































 」と自然に定義できます。
」と自然に定義できます。  を
を 乗すると
乗すると
 になることを利用しています。
になることを利用しています。













































 」と自然に定義できます。
」と自然に定義できます。  を
を 乗すると
乗すると
 になることを利用しています。
になることを利用しています。除算も、式変形を繰り返すことで「





































































 」と自然に定義できます。
」と自然に定義できます。






































































 」と自然に定義できます。
」と自然に定義できます。以上をまとめると、図1-2の通りになります。
乗算と除算は複雑で、綺麗な式とは言いがたいですが、実はこの式が平面上の回転操作になっています。 試しにこれから複素数を平面で表して確認してみましょう。
2複素平面
2.1複素平面
複素数「


 」を「
」を「



 」という点だとみなすと、複素数全体は平面を作ります。 この平面を「複素平面」といいます(図2-1)。
」という点だとみなすと、複素数全体は平面を作ります。 この平面を「複素平面」といいます(図2-1)。



 」を「
」を「



 」という点だとみなすと、複素数全体は平面を作ります。 この平面を「複素平面」といいます(図2-1)。
」という点だとみなすと、複素数全体は平面を作ります。 この平面を「複素平面」といいます(図2-1)。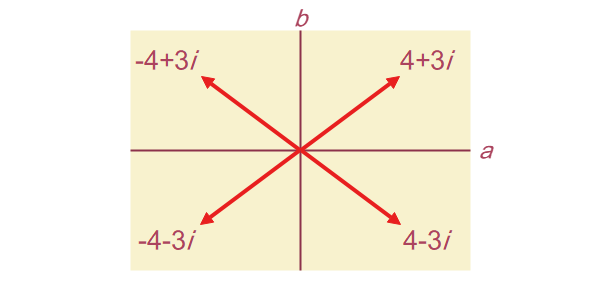
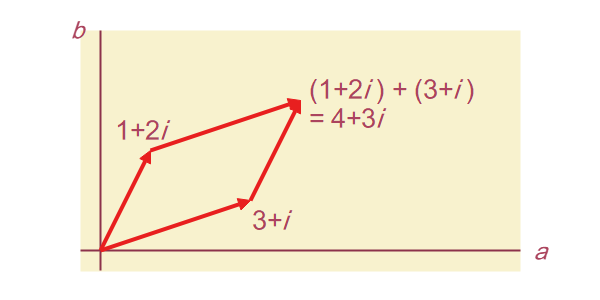
先ほど定義した演算では、加算とスカラー倍が成り立つため、ちょうど第10話で説明したベクトルの一種だといえます(図2-2)。
ただし複素数には、ベクトルには無かった乗算と除算が定義されていて、これらは複素平面上の回転操作になります(図2-3)。
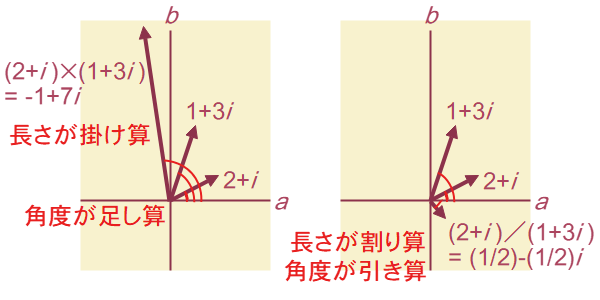
2つの複素数を乗算すると、この図のように矢印の長さは掛け算したものになり、矢印の角度は足し算したものになります。 また除算では、矢印の長さは割り算したものになり、矢印の角度は引き算したものになります。
このように乗算と除算が回転操作になっていることから、回転運動や周期的な波を表す分野でよく使われています。
2.2複素共役と絶対値
さて、他に複素数でよく行われる演算として、「複素共役」と「絶対値」があります。
「複素共役」とは、複素数「


 」に対し、
」に対し、 の符号をマイナスにして「
の符号をマイナスにして「


 」とすることです。 複素共役は複素平面において上下を反転させるため、乗算で考えると逆回転を意味します。
」とすることです。 複素共役は複素平面において上下を反転させるため、乗算で考えると逆回転を意味します。



 」に対し、
」に対し、 の符号をマイナスにして「
の符号をマイナスにして「


 」とすることです。 複素共役は複素平面において上下を反転させるため、乗算で考えると逆回転を意味します。
」とすることです。 複素共役は複素平面において上下を反転させるため、乗算で考えると逆回転を意味します。複素共役は多くの場合、変数の上に横線を書いて表します。 例えば、




 の複素共役は
の複素共役は




 で、
で、




 の複素共役は
の複素共役は




 です。
です。





 の複素共役は
の複素共役は




 で、
で、




 の複素共役は
の複素共役は




 です。
です。「絶対値」とは実数にも定義されていましたが(符号を正にする演算)、複素数では矢印の長さを得る演算で、複素数「




 」に対し、その絶対値は「
」に対し、その絶対値は「



 」と定義されます。
」と定義されます。  が
が のときには、複素数の絶対値は実数の絶対値と一致します。 例えば、
のときには、複素数の絶対値は実数の絶対値と一致します。 例えば、




 の絶対値は
の絶対値は





 です。
です。





 」に対し、その絶対値は「
」に対し、その絶対値は「



 」と定義されます。
」と定義されます。  が
が のときには、複素数の絶対値は実数の絶対値と一致します。 例えば、
のときには、複素数の絶対値は実数の絶対値と一致します。 例えば、




 の絶対値は
の絶対値は





 です。
です。またこの絶対値は、複素共役を使って「





 」が成り立ちます。 「
」が成り立ちます。 「
























 」となるためです。 複素数の式が複雑な形になると「
」となるためです。 複素数の式が複雑な形になると「


 」の
」の と
と に分離することが大変になるため、
に分離することが大変になるため、



 の代わりに、
の代わりに、

 が出てこない「
が出てこない「





 」で絶対値を求めることがよく行われます。
」で絶対値を求めることがよく行われます。






 」が成り立ちます。 「
」が成り立ちます。 「
























 」となるためです。 複素数の式が複雑な形になると「
」となるためです。 複素数の式が複雑な形になると「


 」の
」の と
と に分離することが大変になるため、
に分離することが大変になるため、



 の代わりに、
の代わりに、

 が出てこない「
が出てこない「





 」で絶対値を求めることがよく行われます。
」で絶対値を求めることがよく行われます。3複素関数
ここからは、


 や
や
 などの関数を複素数に拡張していきます。 とはいえ「
などの関数を複素数に拡張していきます。 とはいえ「


 」のようなものを考えたとしても、角度が「
」のようなものを考えたとしても、角度が「 」とはどういうことかよく解らないと思いますが、複素数に拡張することで関数の意外な性質が見つかるかもしれないため、ひとまずは深く考えずに拡張してみましょう。
」とはどういうことかよく解らないと思いますが、複素数に拡張することで関数の意外な性質が見つかるかもしれないため、ひとまずは深く考えずに拡張してみましょう。



 や
や
 などの関数を複素数に拡張していきます。 とはいえ「
などの関数を複素数に拡張していきます。 とはいえ「


 」のようなものを考えたとしても、角度が「
」のようなものを考えたとしても、角度が「 」とはどういうことかよく解らないと思いますが、複素数に拡張することで関数の意外な性質が見つかるかもしれないため、ひとまずは深く考えずに拡張してみましょう。
」とはどういうことかよく解らないと思いますが、複素数に拡張することで関数の意外な性質が見つかるかもしれないため、ひとまずは深く考えずに拡張してみましょう。3.1テイラー展開
関数を複素数に拡張するとき、「


 」の
」の が
が のときには実数と一致するように拡張します。 これを自然に行う方法として、「テイラー展開」があります。
のときには実数と一致するように拡張します。 これを自然に行う方法として、「テイラー展開」があります。



 」の
」の が
が のときには実数と一致するように拡張します。 これを自然に行う方法として、「テイラー展開」があります。
のときには実数と一致するように拡張します。 これを自然に行う方法として、「テイラー展開」があります。「テイラー展開」とは、関数を四則演算の組み合わせに展開する方法です。 ここまでで複素数の四則演算は定義しましたので、関数を四則演算に展開できれば自然に複素数にも拡張できるはずです。 テイラー展開は、図3-1の通りです。
無限回微分可能な関数


 と実数
と実数 に対して、以下の右辺が収束し、また
に対して、以下の右辺が収束し、また



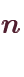













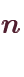

 を満たす
を満たす が存在するとき、以下の等式が成り立つ。
が存在するとき、以下の等式が成り立つ。














































































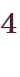













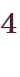


テイラー展開は数式で書くと複雑ですが、要するに関数の微分を行えば、あとは四則演算のみの組み合わせに展開できるということです。
ちなみにこの数式に出てくる
 は、
は、 の「階乗」と呼ばれ、
の「階乗」と呼ばれ、










 です。 例えば
です。 例えば の階乗は、
の階乗は、














 です。
です。

 は、
は、 の「階乗」と呼ばれ、
の「階乗」と呼ばれ、










 です。 例えば
です。 例えば の階乗は、
の階乗は、














 です。
です。それでは「


 」をテイラー展開してみましょう。 「
」をテイラー展開してみましょう。 「







 」とおいて第7話の微分を使うと、
」とおいて第7話の微分を使うと、 階微分は「
階微分は「









 」となり、
」となり、 階微分は「
階微分は「










 」となるため、そのまま何度も微分を繰り返して上記の数式に代入すると、図3-2のように展開できます。
」となるため、そのまま何度も微分を繰り返して上記の数式に代入すると、図3-2のように展開できます。



 」をテイラー展開してみましょう。 「
」をテイラー展開してみましょう。 「







 」とおいて第7話の微分を使うと、
」とおいて第7話の微分を使うと、 階微分は「
階微分は「









 」となり、
」となり、 階微分は「
階微分は「










 」となるため、そのまま何度も微分を繰り返して上記の数式に代入すると、図3-2のように展開できます。
」となるため、そのまま何度も微分を繰り返して上記の数式に代入すると、図3-2のように展開できます。







 とおくと、
とおくと、


































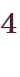











 より、
より、





































































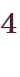

























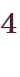





つまり、「













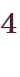
















 」となります。 簡単に確かめてみましょう。 本来は「
」となります。 簡単に確かめてみましょう。 本来は「






















 」の値ですが、テイラー展開後の式を計算していくと表3-1のようになります。
」の値ですが、テイラー展開後の式を計算していくと表3-1のようになります。














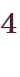
















 」となります。 簡単に確かめてみましょう。 本来は「
」となります。 簡単に確かめてみましょう。 本来は「






















 」の値ですが、テイラー展開後の式を計算していくと表3-1のようになります。
」の値ですが、テイラー展開後の式を計算していくと表3-1のようになります。| 式 | 値 |
|---|---|
 |
 |
           |
           |
                 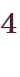    |
           |
                 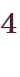              |
           |
                 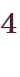                        |
           |
                 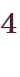                                    |
           |
テイラー展開の値が元の関数の値(









 )に近づいていくことが分かります。 確かに四則演算の組み合わせに展開できているようです。
)に近づいていくことが分かります。 確かに四則演算の組み合わせに展開できているようです。










 )に近づいていくことが分かります。 確かに四則演算の組み合わせに展開できているようです。
)に近づいていくことが分かります。 確かに四則演算の組み合わせに展開できているようです。さてそれでは、逆にテイラー展開後の式から元の関数を定義し直す流れで、複素数に拡張しましょう。 任意の複素数 に対し、「
に対し、「













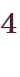
















 」と定義します。
」と定義します。
 に対し、「
に対し、「













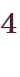
















 」と定義します。
」と定義します。例えば、「


 」の値を求めると表3-2のようになります。
」の値を求めると表3-2のようになります。



 」の値を求めると表3-2のようになります。
」の値を求めると表3-2のようになります。| 式 | 値 |
|---|---|
 |
 |
       |
   |
         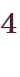    |
           |
         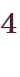          |
           |
         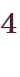                |
           |
         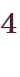                        |
           |
         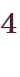                                |
           |
「














 」となることが分かりました。
」となることが分かりました。















 」となることが分かりました。
」となることが分かりました。3.2複素関数とオイラーの公式
さて、同様に


 や
や
 もテイラー展開して複素数に拡張すると、図3-3のようになります。
もテイラー展開して複素数に拡張すると、図3-3のようになります。



 や
や
 もテイラー展開して複素数に拡張すると、図3-3のようになります。
もテイラー展開して複素数に拡張すると、図3-3のようになります。複素数 について、
について、










 を以下のように定義する。
を以下のように定義する。
すると、
 は、
は、


 と
と


 を組み合わせたものに見えてこないでしょうか。 実際、
を組み合わせたものに見えてこないでしょうか。 実際、


 の代わりに
の代わりに



 とし、
とし、
 の代わりに
の代わりに

 のように少し変形すると、図3-4のようになります。
のように少し変形すると、図3-4のようになります。

 は、
は、


 と
と


 を組み合わせたものに見えてこないでしょうか。 実際、
を組み合わせたものに見えてこないでしょうか。 実際、


 の代わりに
の代わりに



 とし、
とし、
 の代わりに
の代わりに

 のように少し変形すると、図3-4のようになります。
のように少し変形すると、図3-4のようになります。以上から

 は、
は、


 と
と



 を足し合わせたものになっています。 よって、「
を足し合わせたものになっています。 よって、「












 」が成り立つことが分かります。 この定理を「オイラーの公式」といいます。
」が成り立つことが分かります。 この定理を「オイラーの公式」といいます。


 は、
は、


 と
と



 を足し合わせたものになっています。 よって、「
を足し合わせたものになっています。 よって、「












 」が成り立つことが分かります。 この定理を「オイラーの公式」といいます。
」が成り立つことが分かります。 この定理を「オイラーの公式」といいます。一見無関係そうな「
 」と「
」と「


 」「
」「


 」が、複素数に拡張したことで繋がりました。
」が、複素数に拡張したことで繋がりました。

 」と「
」と「


 」「
」「


 」が、複素数に拡張したことで繋がりました。
」が、複素数に拡張したことで繋がりました。3.3オイラーの等式
また、オイラーの公式「












 」の
」の に
に を代入すると、有名な「オイラーの等式」すなわち「
を代入すると、有名な「オイラーの等式」すなわち「





 」が導けます。
」が導けます。













 」の
」の に
に を代入すると、有名な「オイラーの等式」すなわち「
を代入すると、有名な「オイラーの等式」すなわち「





 」が導けます。
」が導けます。この式は「最も美しい定理」などと言われることもあり、ネイピア数「 」、虚数単位「
」、虚数単位「 」、円周率「
」、円周率「 」、乗法の単位元「
」、乗法の単位元「 」、加法の単位元「
」、加法の単位元「 」が並ぶ様は絶景ですが、複素数の乗算が回転操作になっていることと、その回転に関わる三角関数
」が並ぶ様は絶景ですが、複素数の乗算が回転操作になっていることと、その回転に関わる三角関数







 が指数
が指数
 と複素数に拡張したときに繋がることが魅力の根底にあると思います。
と複素数に拡張したときに繋がることが魅力の根底にあると思います。
 」、虚数単位「
」、虚数単位「 」、円周率「
」、円周率「 」、乗法の単位元「
」、乗法の単位元「 」、加法の単位元「
」、加法の単位元「 」が並ぶ様は絶景ですが、複素数の乗算が回転操作になっていることと、その回転に関わる三角関数
」が並ぶ様は絶景ですが、複素数の乗算が回転操作になっていることと、その回転に関わる三角関数







 が指数
が指数
 と複素数に拡張したときに繋がることが魅力の根底にあると思います。
と複素数に拡張したときに繋がることが魅力の根底にあると思います。今回は、2乗すると負になる数を説明しました。 次回は、基本編の最終回、ゴムのように伸び縮みする軟らかい立体を扱います!